

アンドリュー・ワイルズ ピエール・ド・フェルマー


上のアンドリュー・ワイルズの写真の、黒板に書いてあるのがフェルマーの定理(予想)です。フェルマーの最終定理とは、3 以上の自然数 n について、x^n + y^n = z^n となる自然数の組 (x, y, z) は存在しないという定理のことである。フェルマーの大定理とも呼ばれる。フェルマーが驚くべき証明を得たと書き残したと伝えられ、長らく証明も反証もなされなかったことからフェルマー予想とも称されたが、360年後にアンドリュー・ワイルズによって完全に証明され、ワイルズの定理あるいはフェルマー・ワイルズの定理とも呼ばれるようになった。本書の入る前に、フェルマーとワイルズの紹介を行っておこう。ピエール・ド・フェルマー(1607年- 1665年1月12日)はフランスの数学者で「数論の父」とも呼ばれる。ただし、職業は弁護士であり、数学は余暇に行ったものである。1607南フランスのトゥールーズ近くのボーモン=ド=ロマーニュに生まれ、1631年 - トゥールーズの請願委員となり、母の従姉妹のルイズ・ド・ロンと結婚。1648年 - トゥールーズ議会の勅撰委員となる。数学においては、パスカルと共同で確率論の基礎を作り、デカルトと文通を交わしながらデカルトとは独立に解析幾何学を創案するなどの功績を残す。 解析幾何学については、デカルトが二次元での理論にとどまったのに対し、フェルマーは三次元空間でも考えていた。その他、幾何学、微分積分学といった諸分野においても先駆的な仕事を遺しており、特に数論における仕事は独創的で後世の数論家たちに大きな影響を与えた。数論への傾倒の直接的な契機は、古代ギリシャの数学者ディオファントスが著した『算術』 (Arithmetica) の注釈本を1630年ごろに手に入れて研究したことのようである。 『算術』を熟読していくうちに彼はその余白に有名な48の注釈を書き込んだ。 フェルマーの数論における仕事が世に知られるようになったのは、その死後に長男のサミュエルが『算術』を父の書込み付きで再出版してからであり、数論の研究においては事実的に孤立していた。48の書込みのうち47の命題は後世の数学者達によって証明または反証が与えられたが、最後の一つは長年にわたって解かれずにいた。最後に残された、という意味でフェルマーの最終定理とも呼ばれるようになった有名な命題であるが、誰一人として証明も否定も成功せず、360年にわたって数学の謎の一つであり続けた。この問題は最終的に1995年、アンドリュー・ワイルズが谷山・志村予想の一部を証明したことによってようやく解決され、20世紀数学の掉尾を飾る金字塔となった。フェルマーが「真に驚くべき証明を発見した」と記しているフェルマーの最終定理についても、フェルマーは本当に証明していたかどうかは不明である。
アンドリュー・ワイルズ(1953年4月11日 - )は、イギリスの数学者。オックスフォード大学教授(整数論)。10歳のときにフェルマーの最終定理に出会い数学の道を進む。ケンブリッジ大学卒業。大学院でジョン・コーツの指導のもと、岩澤理論と楕円曲線論の研究、博士号を取得した。1989年王立協会フェロー選出され、プリンストン大学教授を経て、2011年から現職。証明に挑んだきっかけは、ケン・リベットが「フライの楕円曲線(=フェルマーの最終定理の反例)」はモジュラーとはならないことを証明したと聞き、フェルマーの最終定理を証明するには谷山・志村予想(従ってフライの「楕円曲線」は存在しないことを意味する)を解けば良いことを知ったことだった。もともと自身が数学を志したきっかけが少年時代にフェルマーのこの定理と出会ったことであり、この定理に対しては強い憧れを持っていたが、大学院時代に数々の天才が挑んでは敗れ去ってきたこの超難問に挑戦することを指導教官のコーツから止められていた。それが、上述のような経緯で自ら専門分野の楕円曲線と思いがけずも繋がることとなり、谷山・志村予想の証明だけに没頭することになったという。やがて3年目に、楕円曲線をガロア曲線に変換して比べたり、岩澤理論を応用したりして類数公式を考えることを思いついたものの、証明には手が届かなかった。ある日、フラッハ(→コリヴァギン=フラッハ法)という学生の論文に出会い、今までの考えを捨ててその理論を拡張することに専念するようになる。やがて7年目に、バリー・メイザーの論文から、モジュラーでない楕円曲線をモジュラーである楕円曲線に変換することを考え、フェルマーの最終定理の証明を確信した。最初の発表の場であったケンブリッジ大学の講演(1993年6月21?23日)では、事前にフェルマーの定理を証明したと告知していたわけでないにもかかわらず、噂が噂を呼んで、ジョン・コーツ、バリー・メイザー、リチャード・テイラーなど、多くの数学関係者が押しかけてきた。教室は満席で、立ち見まで出るほど盛況だったという。講演を終えた後、証明を論文誌に投稿したが、レフリーからの指摘で1箇所、致命的なギャップが発見された。それまでの単独研究というスタイルを捨て、弟子であるリチャード・テイラーも加えて、このギャップを埋めようとしたが難航した。多くの注目を集める中での研究となり、一時期は敗北宣言を出すことまで考えた。1994年9月19日、自身で諦めをつけるために証明のうまくいかない部分を見直していたところ、突然インスピレーションが涌き、本人曰く「夢じゃないかと思うような素晴らしい証明」が頭に浮かんだ。それは、うまくいかなくしている、まさにその原因が、研究当初放棄した岩沢理論によるアプローチを可能にするという発見であった。翌日、もう一度冷静に見直した結果、誤りがないことを確認し、証明を完成させた。新たな論文は1995年のAnnals of Mathematicsに掲載された。再度の審査の結果、証明は確認され、ワイルズのフェルマー予想解決が認められた。この予想がフェルマーによって提起されてから実に360年後のことであった。国際数学連合のフィールズ賞には40歳以下という制限があるため受賞を逃したが、その顕著な業績に対して異例の特別賞が贈られた。
著者サイモン・シン氏のプロフィールを紹介する。サイモン・レーナ・シン(1964年1月1日 - )は、プロデューサー、ジャーナリスト、サイエンス・ライター。インドパンジャーブからの移民である両親を持ち、イギリス南西部サマーセット州に生まれる。 インペリアル・カレッジ・ロンドンで学び、その後ケンブリッジ大学大学院にて素粒子物理学の博士号を取得。 のちにテレビ局BBCに就職し、ドキュメンタリー番組『フェルマーの最終定理――ホライズンシリーズ』にて各種の賞を受賞した。後にこの番組はエミー賞にもノミネートされた。この時の取材を元に書下した「フェルマーの最終定理」(本書)も高い評価を受けベストセラーとなる。 受賞歴は1996年 - 英国アカデミー賞、2003年 - 大英帝国勲章、名誉博士号(ラフバラー大学)、2005年 - 名誉博士号(サザンプトン大学)、2008年 - ケルヴィン・メダル(イギリス物理学会)を受けた。
翻訳者青木薫氏のプロフィールを紹介する。青木氏は1956年山形県生まれ、京都大学理学部卒業、1984年同大学院博士課程修了、「原子核間ポテンシャルのパリティ依存性及び角運動量依存性に関する微視的研究」で理学博士。専門は理論物理学。2007年度日本数学会出版賞受賞。科学書の翻訳家でなる。翻訳書は今までに60冊を超えている。著書には「宇宙はなぜこのような宇宙なのか 人間原理と宇宙論」(講談社現代新書 2013)がある。
フェルマーの最終定理(17世紀 フランス)を遡れば、デイオファントスの「算術」(紀元前3世紀 アレクサンドリア)にあり、デイオファントスの算術を遡ればピタゴラス数(紀元前6世紀 ギリシャ)が源泉となる。そこでピタゴラス数すなわち、直角三角形の3つの整数の辺の長さについて、大矢真一著 「ピタゴラスの定理」(東海大学出版会 2001年8月)よりまとめておこう。三つの辺の長さがすべて整数でありa^2+b^2=c^2を満たす直角三角形の辺の組のことを「ピタゴラス数」という。大昔どうして見つけたのかは一切明らかではない。そこで推測であるが、第1段でその整数の二乗を順に書いてゆく。第2段で二乗の数の差を一つ置きに求める。ピタゴラスの四角数と同じようにすると
第1段: 0 1 4 9 16 25 36 49 64 81 100 121 144 169・・・・・
第2段: 4 8 12 16 20 24 28 32 36 40 44 38 52・・・・・
3^2+4^2=5^2より(3,4,5)、6^2+8^2=10^2 より(6,8,10)=(3,4,5) また8^2+15^2=17^2より(8,15,17)などが得られる。これからすべてのピタゴラス数が得られるはずであろうが、大変なことである。もう少し規則的な方法はないのだろうかと古来いろいろな公式が工夫されてきた。ピタゴラスの方法(推測)は前に示した。プラトン、プロクルス、ユークリッド・ジオファントス、ジオファントスの方法がある。そこで最もポピュラーなユークリッド・ジオファントスの方法によるピタゴラス数の求め方を示す。
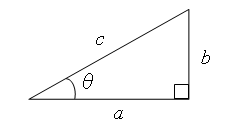
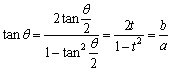 ②
②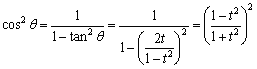 ∴
∴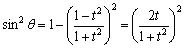 ∴
∴①②③より、 a = k(1 - t^2) ,b = k・2t ,c = k(1 + t^2) …④
a, b, cは自然数なので t は有理数である。よってt = n / m …⑤
とおくことができます。ここでm, n は互いに素であり、0 < t < 1 より0 < n < m となります。④⑤より、
a = k(1 - t^2) = k(1 - n2/m2) = k/m^2 (m^2 - n^2) = k'・(m^2 - n^2)
b = k・2t = k(2 ・ n/m) = k/m^2 ・ 2mn = k'・2mn
c = k(1 + t^2) = k(1 + n^2/m^2) = k/m^2 (m^2 + n^2) = k'・(m^2 + n^2)
ここで、m - n は奇数としてよい。これらのことからピタゴラス数は、
こうしてディオファントスは無限に存在するピタゴラス数を求める一般的な方法を示した。(a,b,c)という辺の長さの二乗の関係式がピタゴラスの定理であり、ここまでは幾何学であった。つぎにディオファントス方程式とは、整係数多変数高次不定方程式である。主に数論の研究課題と考えられている。古代アレクサンドリアの数学者ディオファントスの著作『算術』で、その有理数解が研究されたのにちなんだ名称である。ピタゴラスの方程式(2次)、楕円曲線(3次、4次)もディオファントス方程式の特殊例であった。フェルマーの最終定理とは、3 以上の自然数 n について、x^n + y^n = z^n となる自然数の組 (x, y, z) は存在しないという定理のことである。本書の目的はフェルマーの最終定理の証明を厳密に述べることではない。そんなことを書いても数学者でさえ理解できるのは1割くらいであり、一般読者では理解できる人は皆無であろうと思われる。だから本書は17世紀以降の数論に寄与した数学者の業績と、フィルマ―の最終定理に関係した現代数学者の群像を描くことである。
1) ピタゴラスの定理からフェルマーの最終定理へ1993年6月23日、ケンブリッジ大学のアイザック・ニュートン研究所で数学の特別講演会が行われた。セミナーの題目は「L関数と数論」であった。講師はプリンストン大学教授でイギリス人のアンドリュー・ワイルズである。時にワイルズの年齢は40才の大台に乗っていたし、この7年間数学界ににはめっきり姿を見せなかったため、もうワイルズの数学者としての寿命はかれてしまったのかと噂されていた。実はワイルズはこの7年間というもの、数学最大の問題を解決すべく完全な秘密のうちに研究を続けていたのであった。数学者アルフレッド・アーサーは「数学者の数学的寿命は短い。25才、30歳を過ぎると成果を上げられる見込みはない」とさえ言う。ハーディーも「若い人は定理の証明をすべきであり、老人は本を書くべきである」という。王立協会の会員になる年齢は数学者が一番低い。ラマヌジャンは31才で王立協会会員になった。19世紀のノルウエー人アーベルは20才で代数学の畢竟の大仕事をし、ガロアも10代で大きな仕事を成し遂げ21歳で世を去った。ワイルズが秘密主義を取ったのは成果の独り占めであるが、反面大きなつけを払わなくてはならない。それは自分のアイデアを数学者と協議し検証したりして、大きな誤りを未然に防ぐことができないという可能性があるということである。ワイルズは1963年10歳のころから数学の問題の虜になっていた。ワイルズ少年は近くの図書館に通って、ベルによる「最後の問題」という数学の歴史が書かれており、17世紀フランスのフェルマーが遺した問題に夢中になった。フェルマーの最終定理とはピタゴラスの定理に基づいており「直角三角形の斜辺の二乗は、他の二辺の二乗の和に等しい」から出発している。ピタゴラスは紀元前6世紀の古代ギリシャ人で、サモスの賢者といわれ「数には数の論理がある」という思想を抱き、ミロンの援助のもと秘密の数学者集団「ピタゴラス教団」を設立した。弟子の数は600人ほどで、数を神とする宗教集団の様であった。自然数と分数(二つ合わせて有理数をつくる)に関心を寄せた。なかでも「完全数」(その数の約数の和がその数に等しい) たとえば6の約数は1,2,3でありその約数の和は1+2+3=6であり元の数の同じになる。そして完全数は常に連続した自然数の和にひとしい。6=1+2+3、28=1+2+3+4+5+6+7・・・である。そして完全数は2のベキ数と密接な関係にあり、2のベキ数の約数の和はつねにその数より1少ないことを見出した。2の2乗=4 約数の和 1+2=3 2の3乗=8 約数の和 1+2+4=7 2の4乗=16 約数の和 1+2+4+8=15・・・である。さらにユークリッドは完全数はつねに二つの数の積で表され、その一方は2のベキ数、片方は2のベキ数から1を引いたものになることを発見した。6=2×3=2^1(2~2-1) 28=4×7=2^2(2^3-1)・・・ピタゴラス数リストに見るように、辺の長さが1少ない二辺の例が多いのもそのせいである。ピタゴラスは自然現象と数の関係にも興味を持ち、自然法則は数式で表せることに気が付いた。特に弦の分割と振動数(音程)の関係は顕著である。円の直径と円周の比が一定であること(円周率π)は古代エジプト人の発見による。ピタゴラスは「万物は数なり」と言い切った。数学の定理は、一連の公理から出発し論理的なプロセスを経て得られた結論が定理である。この点が仮説を設ける物理学とは本質的に異なる。こういう数学の論理が古代ギリシャ時代から構築されていたことは驚異である。ピタゴラスの定理は幾何学的要素が強かったが、時代が進むにつれ代数学要素(関数方程式)が強くなった。二つの整数の二乗の和が一つの整数の二乗に等しい解の組み合わせをピタゴラス数(a,b,c)といい、その組み合わせは無限にある。ピタゴラス数の命題の一般化はベキ数を3以上にすることから始まった。x^3+y^3=z^3の整数の解があるのかであった。どうやら3乗の方程式を満たすような3つの数は求まらなかった。17世紀のフランスの数学者フェルマーは、誰にも解が見つけられないのは解が存在しないからだという主張をしたのだ。そしてフェルマーから300年あまり、世界の数学者は書かれなかった証明法をめぐって悪戦苦闘したがその試みはすべて失敗に終わった。その証明法が1993年6月23日、ワインズによってケンブリッジ大学のアイザック・ニュートン研究所で発表された。200名いた聴衆から祝福の喝采があがった。この本はそのサイエンスストーリである。
2) 数論ピエール・ド・フェルマーはフランスグランドセルブのフランシスコ会修道院からトゥールーズ大学に進んだ。役人の道を選び、1631年にはパリにいる王に請願をする時の地域の受付である「請願委員」に任命された。王と地方を結ぶ重要なパイプ役であった。そしてフェルマ―は裁判所の参事官も兼ねていた。フェルマーは社交界の名士となり、トゥールーズ議会の勅選議員に選ばれた。フェルマーはアマチュアの数学者であったが、余りにも優れていたのでプロの数学者として扱われた。その時代数学のアカデミックの地位は低く、生活は自己資金に頼った生活であった。だから17世紀の数学者はほとんどアマチュアであったといえる。欧州で数学を奨励していたのはオックスフォード大学のみで、1619年幾何学のサヴィル講座を創設した。パリではパスカル、ガッサンディ、ロヴェルヴァル、メルセンス神父らが参加する小さな数学者のサークルがあった。当時商人に雇われる計算のプロ職人(今でいう会計士か)がいたが、秘密主義的傾向が強かった。代数学の計算技術として、三次方程式を解くことを発見したタルターリアとジェラモ・カルダーノの喧嘩は有名である。パリにやって来たメルセンス神父はこうした秘密主義と戦い彼らのサークルは「フランス学士院」の中心メンバーとなっていった。メルセンヌがフランスを旅行してフェルマーと接し、フェルマーの目を大きく開かせた。しかしフェルマーが発見した数学上の多くの定理について、メルセンヌ神父が証明を示すように勧めたが、フェルマーは頑として定理を証明付きで開示することはなく、むしろ挑戦的にできるなら証明してみろと言わんばかりであったという。 問題は示すが解法は隠すというフェルマー流のやり方は数学者を困らせ、その定理の証明が難しければ難しいほど彼の名声を獲得するチャンスはなくなり、学界から忘れ去られる危険性の方が高かった。フェルマーとパスカルの文通によって「確率論」の定理が生まれた。またフェルマーは「微積分学」の創始者の一人であった。ニュートンは「フェルマーの接線の引き方」に基づいて微積分法を発明したのである。微積分学と確率論という実用性の高い数学の分野の創設にかかわっただけでなく、フェルマーは何の役にも立たない「数論」を最も愛したと言われる。 ピタゴラスの教団が滅んだあと、200年も経つと数学研究の中心はクロトンからアレクサンドリアに移った。アレクサンドリアに初めて図書館ができたのは、アレクサンドリア大王の将軍だったプトレマイオス1世がエジプト王になった時からのことである。世界中の学術書の写本をアレクサンドリアの図書館に集める使命を負ったのはデメトリオという人物であった。その数学部門の責任者が、ユークリッドであった。ユクリッド(紀元前330年生まれ)が著した「原論」13巻は史上最高のロングセラーとなり、ユークリッドの業績が3巻で、あとは冬至の数学的知識の集大成で会った。そのうち2巻はピタゴラス教団の業績である。ユークリッドが多用した論理のテクニックに「帰謬法」、「背理法」であった。背理法によるユークリッドの証明で一番有名なのは「無理数」の数存在を立証したことである。ピタゴラス教団は無理数(例えば√2や円周率π)を隠蔽して有理数までで考えを束縛した。しかし無理数を小数で表そうとすると、規則性もパターンもない数が無限に続いてしまう。ユークリッドは√2が分数では表記できないことを証明するために背理法を用いた。√2=1.414213562373・・・の少数はあくまで近似値で、永遠に記述することは終わらないのである。ユークリッドは数論に関心を持っていたことは確かであるが、彼の業績は「幾何学」にあった。原論全13巻のうち、第1巻から第5巻までは平面幾何学、第11巻から第13巻までが立体幾何学が扱われている。
数論の領域でユークリッドに匹敵する業績を上げたのはアレクサンドリアのディオファントスの「算術」である。AD250年ごろのアレクサンドリアの人であった。全13巻のうち半分が中世を生き延びてルネッサンス期の数学者に多大な影響を与えた。アレクサンドリアはユークリッドからディオファントスの数世紀間、文明世界の知的首都であった。しかしAD389年キリスト教の皇帝テオドシウスによって破壊され、AD642年征服したイスラム教国によってわずかに残っていた図書館は灰燼に帰した。それから千年近く西洋の数学は沈滞し、その燈火はアラビアやインドで受け継がれた。インドでは数学にゼロという新しい要素が数に加わった。またアラビア数字は計算に便利で広く普及し、ゼロと併せて位取りや計算が非常に容易になった。10世紀になってフランスではスペインのムーア人からこの記数法を学び、西洋に広く伝わった。西欧の数学にとって一大転機となったのは1453年のオスマントルコによるコンスタンチノープル掠奪によって、アレクサンドリから避難してきた書物がまた破壊の危機にさらされた。「算術」の貴重な数巻が西欧へ避難し、デイファントスはフェルマーの机上に登ることになったのである。フェルマーは特定の数学者の影響を受けたという記録はないが、ディオファントスの「算術」がフェルマーを導いた。フェルマーが読んだ「算術」は1621年出版のガスパール・パシェのラテン語訳であった。フェルマーは「算術」の本の余白に、論法やコメントや自分の発見したもっと難しい問題を走り書きをした。フェルマの発見した「友数」という数の問題がある。ピタゴラスの「完全数」と深い関係にある数で、一方の約数の和が、片方の「数の約数の和になるという関係である。たとえば280の約数は1,2,4,71,142でその和は220であり、220の約数は1,2,4,5,10,11,20,22,44,55,110でその和は284である。284と220は友数と呼んだ。ピタゴラス教団は(220、284)しか友数を発見できなかったが、フェルマーは(17296,18416)を発見した。後にデカルトは(9363584、9437056)を発見し、そしてオイラーは何と62組の友数を発見した。20世紀になってこの数論の延長で「社交数」という数の組が発見された。一番目の数の約数の和が2番目の数になり、2番目の数の約数の和が3番目の数になり、3番目の数の約数の和が一番目の数となるというループの関係である。この数の問題(お遊びに近い)はそれほど深い話ではなく他の分野への影響もなかった。ディオファントスは「不揃いの三角形」を構成する3つ組の数について述べている。2つの短辺の値が1しか違わないピタゴラスス数である。無数にあるが中でも(20、21,29)は20^2+21^2=29-2というピタゴラスの定理を満たす数である。この数の組が無数に存在することはユークリッドが証明したことは上の「ユークリッド・ジオファントスの方法」によるリストに示した通りである。フェルマーはピタゴラスの方程式x^2+y^2=z^2を見ている時、突然z^3+y^3=z^3を思いついた。これに解があるのだろうか。もっと一般にはx^n+y^n=z^n (n≧3)の解を求める問題である。そして「算術」の余白に「ある3乗数を2つの3乗数の和で表すことは不可能である」そしてさらに「私はこの命題の真に驚くべき証明を持っているが、余白が狭すぎるのでここには記することはできない」と書いた。この思わせぶりな書き方がフェルマーの真骨頂である。1665年1月12日フェルマーは亡くなったが、フェルマーの書き込みは誰に読ませるために「書かれたわけでもないので、あやうく永遠に失われる運命にあった。長男のサミュエル・フェルマーが5年の歳月を費やして「算術」への書き込みを整理して、1670年「フェルマーによる所見を含むディオファントスの算術」を刊行した。そのメモの確証を取る作業は後世の数学者の宿題となった。18世紀最大の数学者オイラーは「素数定理」の証明に取り組んだ。素数は約数を持たない数で、4n+1,4n-1で表される数である。フェルマーの素数定理とは4n+1で表せる素数は常に2つの2乗数の和となり、4n-1で表される素数はそうは表せないという。オイラーは1749年この素数定理を証明した。フェルマーが遺した定理のどの一つにも厳格な証明がなされなければならない。定理こそは数学の土台である。なぜなら一度証明されればその上に安心して他の定理を築くことができるからだ。フェルマーの定理も万人が納得できる方法で証明されなければ「フェルマーの最終予想」と呼ばれる。証明ができていない問題は多数ある。」「リーマン予想」もそうである。
3) フェルマーの最終予想300年間解けなかったフェルマーの最終定理にワイルズ少年は夢中になった。偉大な数学者が挑んで失敗しているからこそ、この問題に取り組む価値があると考えた彼は、先人たちの方法を調べた。なかでも最も注目すべき数学者は18世紀のスイスバーゼル生まれのレオンハルト・オイラー(1707-1783年)である。この人こそフェルマーの最終定理の解明に向けて大きな一歩を踏み出した偉人なのである。オイラーは欧州では「解析学の権化」と呼ばれた。オイラーにとって幸運だったことは同じバーゼルにベルヌーイ一家が住んでいたことであった。ヨーロッパ中で最も優れた数学者一族の勧めでオイラーは数学者の道を歩み始めた。18世紀のヨーリッパで数学者の価値がようやく認められるようになったのは、アイザック・ニュートン(1642 - 1727年)の業績によるところが大である。17世紀はヨーロッパの科学革命の只中にあった。王侯諸国は科学に実用的な価値を認めて大いに奨励した。オイラーは最初帝政ロシア宮廷に招かれ、そしてプロイセンのベルリン学士院から最後はロシアの女帝エカテリーナの下で数学研究に励んだ。オイラーの業績の中でもっとも偉大なものの一つにアルゴリズムによる方法の開発がある。たとえば月、地球、太陽の3体問題は最初から解けないことは分かっているが、実用的に厳密解ではなく近似解を得るならば、大雑把な答えを設定しアルゴリズムに基づいて計算し、それをアルゴリズムにフィードバックしてより正確な近似解を得るという計算方法である。このプロセスを繰り返せば、軍事目的程度の精度で月の位置が分かるという方法である。今ならコンピューターで数百回の計算は瞬時にできる。漸近的数値解析法と言える。オイラーの興味を引いたケーニヒベルグの町の橋にちなむパズルがある。すべての橋を一度だけ渡るならば川の中島に架かる橋は偶数個あればよい。いわゆる一筆書きの問題をオイラーはネットワークの問題として考えた。ネットワークを点と線だけで表すと、頂点の数+面の数ー辺の数=1というオイラーン関係式を導いた。オイラーはフェルマーの最終定理の問題をネットワークの方法と同じように、n次のピタゴラス方程式のいずれかに解がないことを証明し(フェルマーはn=4で解がないことを証明したという)、背理法の一種である「無限降下法」をつかってn=3にたどり着こうとする方法である。ここでオイラーはおはこの虚数を使った。オイラーによって数の概念が飛躍的に拡大し、理論化された。複素数の数平面が定義された。しかし残念なことにn=3の時しかこの方法は使えなかったので、フェルマーの挑戦には敗北した。フェルマーはn=4次には解がないことを証明し、オイラーはn=3次には解がないことを証明した。それは大きな一歩であったがそれより大きなn次方程式にの前には遅々として進まなかった。n=3,6,9,12,15・・・やn=4,8,12,16,20・・・の場合にはオイラーやフェルマーに方法は成り立つ。n=3は素数である。素数の場合が証明できれば非素数の場合は素数に分解できるから証明できるので大多数の方程式は無視してもいいにもかかわらず、nが素数の方程式はやはり無限に存在する。カント―ルの「無限」の集合の概念に依れば、自然数は無限の大きさを持つように、偶数も自然数と1対1の対応が取れるから無限である。すなわち部分が全体と同じ集合の大きさになる。無限に無限を加えても無限である。有理数と無理数とは1対1に対応させることはできないので、無理数の無限集合は有理数の無限集合より大きいことが示される。無限集合の大小の比較はできるのである。素数理論は応用の少ない分野であるが、1970年頃からマーティン・ヘルマンらは軍隊や外交の暗号文作成と解読にはなくてはならない技術を提供している。フランスの女性数学者ソフィー・ジェルマン(1776-1831年)はフェルマーの最終定理の研究に革命を起こして貢献した。ソフィー・ジェルマンの定理とは、2p + 1 が素数であるような素数 p について、x^p + y^p = z^p が成り立つとき、x, y, z のいずれかが p で割り切らねばならない。たとえば x5 + y5 = z5 が成り立つとき、x, y, z のいずれかは 5 の倍数である。また、この定理に現れる 2p + 1 が素数であるような素数 p をソフィ・ジェルマン素数という。この定理を尊敬するカール・フリードリヒ・ガウスとの書簡の交換の形で発表した。いまnをジェルマンの素数とすると、x^n+y^n=z^nにはおそらく解がないことを証明したのである。その線に沿って1825年ディリクレとルジャンドルの二人は独立に、n=5の時解がないことを証明した。またガブリエル・ラメはn=7の場合を証明した。1847年フランス科学学士院はフェルマーの最終定理の解決にたいしてメダルと賞金を懸けた。ラメとルイ・コーシーが名乗りを上げ解決に近いことを宣言した。コーシーとラメの証明の根本的な問題は、どちらも素因数分解の一意性と呼ばれる性質に依存していた。素因数分解の一意性は紀元前4世紀のユークリッドが発見したものであった。コーシーとラメの方法には虚数が含まれており、虚数には一意性が成り立たたないことを、数論の研究者クンマーが発表した。クンマーはn=31以下のすべての素数については一意性の回避は可能であったが、n=37,59,67(100以下の範囲で)では回避は不可能であることを示した。このような素数を「非正則素数」という。完全な証明を阻む障害となっていた。クンマーが示したのは、当時の数学のテクニックではフェルマーの最終定理は完全には証明できないということであった。
4) 抽象性クンマーの主張でフェルマーの定理は迷宮入りしたかのようであった。数学の最先端はフェルマーの最終定理から離れ、科学の錬金術と同じように忘れ去られた感が強くなった。ところが1908年になってドイツの資本家で数学者のパウル・ヴォルフスケールが新たな刺激をもたらした。彼自身がクンマーの証明を検証し、フェルマーの最終定理の証明は達成不可能のように見えたが、彼は自分の財産をなげうってゲッチンゲン王立協会にヴォルフスケール懸賞が委託された。期限は100年とするものであった。世界中のマチュア数学者がヴォルフスケール懸賞を狙ったが、ますます迷宮に踏み込むだけであった。数論で使われる技法はとても抽象的で、論理を誤って不合理の森に彷徨うことが必至でアマチュアの出る幕ではなかった。ここで本書はサム・ロイド(1841-1911)のパズル・ゲームの理論を展開したことをエピソードとして挿入している。パズルの無秩序さを表す変数Dfの不変量が、あるものを別ものに変換するのは不可能だという時に重要な戦略となる。問題の抽象性の好例がゲーム理論だったというだけで、フェルマーの最終定理に関係した話ではないのでしょ言う略する。数学者は19世紀のクンマーの数論研究の上に立つのではなく、数学の基礎に関心が向かっていた。バートランド・ラッセル、ヒルベルト、クルト・ゲーゲルなど20世紀の大数学者は数学基礎論において、数論はどんな問題を解決できるのか、できないのかを議論し、そうしてフェルマーの最終定理に立ち返ったのである。数理論理学者らは数学の論理構造を研究し始めた。非常に基本的であるがために証明できない命題を公理という。代数の公理の一例として「加法の交換法則」がある。m+n=n+m 子の交換法則を含む億塚の公理が自明と見なされ、とてつもなく複雑な知識体系を丸ごと再構築する作業に数理倫理学者が参加した。ドイツの数学者ヘルマン・ワイルは「論理とは、数学者がっそのアイディアを強健にするための健康法である」と述べている。この計画を率いたのが、ドイツの随一の数学者ダーフィット・ヒルベルト(1862-1943年)である。ヒルベルトは、少数の公理ウィ仮定することによって、数学におけるすべての問題は矛盾なく答えられると確信していた。1900年8月パリで開かれた国際数学者会議で23の未解決問題を提示した。ヒルベルトは「我々は知らねばならない。我々は知るであろう」と宣言した。これをヒルベルト・プログラムと呼ぶ。ゴットローブ・フレーゲ(1848-1925年)がその先頭に立った。フレーゲは「算術の基本法則」で数そのものを定義した。ある集合が3つの要素からできているものはその集合が3に含まれている場合だけである。ところがイギリスの論理学者バートランド・ラッセル(1872-1970年)は論理学の矛盾にぶつかった。フレーゲの集合の概念からラッセルのパラドックスを発見した。「集合は、ある時はそれ自身の部分要素となり、ある時はそうではない」ということである。背理法は数学にはパラドックスはない上に立っている。ところが公理からさえ矛盾が導かれる可能性が出たのである。1910年ラッセルは「プリンピキア・マスマテイカ(数学原理)」を著し、パラドックスを提示した。矛盾を阻止する一つの方法は、集合がそれ自身の集合の要素になることを阻止すればいい。ところが1931年25歳のクルト・ゲーゲル(1906-1978年)は、数学は論理的に完ぺきではあり得ないことを証明した。これを「不完全性の定理」と呼ぶ。定理は2つの定理から構成され、①公理的集合論が無矛盾ならば、証明することも反証することもできない定理が存在する。②公理的集合論の無矛盾性を証明する構成的手続きは存在しない というものであった。つまり無矛盾性はけっして証明できないことで、ゲーデルはヒルベルトプログラムは遂行不可能だということを示したのである。①の定理は「私はウソつきだ」というクレタ人のパラドックスと呼ばれる。数学基礎論のヒルベルト・プログラムとゲーデルの不完全性定理については、C・リード著 彌永健一訳 「ヒルベルトー現代数学の巨峰」(岩波現代文庫 2010年7月) と、ゲーデル著 林晋・八杉満利子訳・解説 「不完全性定理」(岩波文庫 2006年9月) に述べた。1963年スタンフォード大学のコーエンはヒルベルトの23の問題のうち、連続体仮説が決定不可能であることを証明した。これらのことでフェルマーの最終定理の証明に暗雲が垂れ込めた。ひょっとするとフェルマーの最終定理の証明が難しいのではなくて、証明不可能なのではないかという疑心暗鬼である。1930年頃までにフェルマーの最終定理の証明に使える数学手法が底をついていたことも悲観論の生まれる素地であった。戦後のコンピューターの数値計算によってn次方程式の解がないことを、n=1000まで証明していったところで、無限につづくすべてについて証明することはできない。こういうことで数学者はコンピューターの結果は証明とはみなさないのである。オイラーはフェルマーの方程式に似た4変数の4次方程式 x^4+y^4+zx^4=w^4には自然数の解がないと予想した。しかしハーバード大学のノーム・エルキースはその解を求めかつ無数の解があることを証明した。1791年15歳のカール・ガウスが出した「過大評価素数予想」(素数の出現頻度が減ってゆくことを予想したが、いつも結果は多い目の予想だった)を、1914年ケンブリッジ大学のJ・Eリトルウッドが十分大きな素数の領域ではガウス予想は過少になること、そして1933年にはS・スキュースが過少になる境界の素数の大きさを決定した。ということで偉大な数学者の予想が外れることもしばしばあるので、フェルマーの最終定理(予想)も外れかも知れない。1975年、さてここからケンブリッジ大学大学院生となったアンドリュー・ワイルズの数学研究者としての第1歩に入ろう。大学院の数学指導教官はジョン・コーツであった。フェルマーの最終定理に取り組むまえに、プロの数学者として実際的なテクニックを学ばなければならない。既存の方法は130年前から停滞したままであった。そこでワイルズはフェルマーの最終定理は棚上げにして、コーツ先生の指導により「楕円曲線論」をテーマとした。注意すべきは、それは楕円という幾何学的な曲線ではなく、y^2=x^3+ax^2+bx+c(a,b,cは任意の整数)の方程式の事である。こういった方程式はかって楕円の周や惑星軌道の長さの計算に用いられたことから命名された。楕円方程式に整数解があるかどうかの見極めは非常に難しい。簡単な例でa=0,b=0,c=2の場合、y^2=x^3-2の整数解は(y=5,x=3)だけである。この証明をフェルマーがやった。25(=5^2),26,27(=3^3)という有名な数列である。2乗と3乗に挟まれた唯一の数が26である。一般的な楕円方程式のa.b.cの値をかえるだけで、独自の性質を持つ方程式が生まれ、しかもそのすべてが解ける領域に属している。たとえばx^3-x^2=y^2+yを正攻法で行っても勝ち目はない。解(x,y)として(0,0)あるいは(1.0)は解であることは容易にわかる。それ以外の解では有限な数の中で解を求めるならば、剰余を法とする系列化がある。先の楕円方程式の解の個数はE5=4(5を法とする解は4個)と呼ぶ。楕円方程式から導出された系列をE系列と呼ぶ。こうしてワイルズとコーツは楕円方程式とE系列についての数論専門家としての地位を確立した。
5) 背理法 谷山・志村予測ここでフェルマーの最終定理の証明にカギを握ることになる日本人数学者、東京大学の谷山豊、志村五郎の業績(楕円方程式のモジュラー型式)について述べておかなければならない。谷山は127年の生まれ、志村はその2年下であった。この二人が数学史の流れを変えるパートナーシップを組むのである。1954年に初めてであった頃大学の数学科は立ち直っていなかった。だから自分たちで勉強をし、「モジュラー形式」のセミナーを開いた。数論研究者のマルティン・アイヒラ―は数学の基礎演算を、加法、減法、乗法、除法、モジュラー形式だと述べた。数学的対象に何らかの変換を施しても全く変化がない性質を対称性と呼ぶたとえば正方形は回転対称性、鏡面対称性、併進対称性を持つことは容易に理解できる。1970年イギリスの物理学者ベンローズは二つの複雑な形状を持つタイルを考案し、無限の平面に敷き詰めることができることを示した。また1984年アルミとマンガンの合金の準結晶がベンローズのタイル張りと同じ構造を持つことが分かった。モジュラー形式は無限の対称性を持つ。谷山と志村の研究したモジュラー形式は、併進、切り替え、交換、鏡映、回転に対して高い対称性を持つ。しかしモジュラー形式は抽象性の高い、二つの複素軸で定義される。モジュラー形式はこの複素空間の上半分に存在し、この空間が4次元(x1,x2,y1,y2)だということである。この4次元を空間を「双曲線空間」という.。双曲線空間に存在するモジュラー形式には、いろいろのものがあるがすべては同じ構成要素からなる。その構成要素の数によってモジュラー形式のつがいが生み出される。これをM系列、すなわちモジュラー系列で表される。モジュラー形式という領域は数学の中でも他の領域とのつながりが極めて弱い。モジュラー形式と楕円方程式は恐ろしくかけ離れた世界であったし、誰も少なくとも関連性があるとは考えなかった。ところが谷村と志村は楕円方程式とモジュラー形式とは実質的に同じではないかと言いだして数学界に衝撃を与えた。1955年日光で行われた数学国際シンポジウムにおいて谷山は、どの楕円方程式も何らかの方法で保型形式と関係づけられるのではないかという提議であった。谷山はドイリングやアイヒラ―ラの研究を調べることによって、2,3の楕円方程式のE系列は保型形式のM系列に対応していること発見した。この発見は直ちにすべての楕円方程式に関連するとは言い難かった。谷村は楕円方程式は皆モジュラー形式とつながっていると提案したのである。電磁気学における、アインシュタインの特殊相対性理論を生んだ電界と磁界の関係と似ている。ところが谷山は31才の1958年結婚をまじかにして自殺した。理論の完成を待たず惜しむべき日本の天才数学者を失った。はじめこの予想は「谷山・志村予想」と呼ばれた。谷山・志村の予想を西洋に紹介したのは20世紀数論の祖アンドレ・ヴェイユで「谷山・ヴェイユ予想」、或は「ヴェイユ予想」と呼ばれるようになった。谷山・志村予想は、「すべての有理数体上に定義された楕円曲線はモジュラーであろう」という数学の予想で後に証明されて定理となったので、モジュラー性定理またはモジュラリティ定理 と呼ばれることもある。1960年代のころ、プリンストン高等研究所のロバート・ラングランスは、谷山・志村予想に込められた内容に衝撃を受け、数学の統一に向けた数多くの予想問題を一つ一つ証明してゆくラングランス・プログラムを提唱し世界中の数学者の参加を呼び掛けた。1970年代にはこのプログラムは数学の未来像の青写真となったが、残念ながら現実的アイデアを持つ数学者がいなくて立ち消えになった。1984年ドイツシュワルツヴァルトで数論研究者のシンポジウムが開かれた。楕円方程式がテーマであった。そこでゲルハルト・フライが何の確証もなかったが、谷山・志村予想を証明することがそのままフェルマーの最終定理の証明につながるという驚くべき主張をしたのである。フライはフェルマーの解A,B,Cがあるなら、並べ替えられた方程式はy^2=x^3+(A^N-B^N)x^2-A^NB^Nという形をとるはずだという。そしてこの方程式は楕円方程式であることを示した。もしもフェルマーの方程式に解があるなら、フェルマーの最終定理は成り立たたず、並べ替えられた方程式が存在するはずだという、背理法を提言した。こうしてフライはフェルマー方程式を楕円方程式に変形することによって、フェルマーの最終定理を谷山・志村予想に結び付けたのである。もしあるとすればフライの楕円方程式が余りに異常な方程式でモジュラー形式に結び付きそうにない。フライの論理をまとめると次のような仕組みになる。
① もしもフェルマーの定理が成り立たたないならば、その場合はフライの楕円方程式が存在する。
② フライの楕円方程式は極めて異常な性質を持つので、モジュラーではありえない。
③ 谷山・志村予想によると、すべての楕円方程式はモジュラーでなければならない。
④ ゆえに、谷山・志村予想は成立しない。
さらに重要なことは、この論理を逆転させられることである。すると次に様な論理展開となり、フェルマーの最終定理の真偽が、谷山・志村予想が証明できるかどうかにかかっているというドラマティックな結論を導いた。
1') もし谷山・志村予想が証明できれば、すべての楕円方程式はモジュラーでなければならない。
2') もしもすべての楕円方程式がモジュラーなら、フライの楕円方程式は存在しえない。
3') フライの楕円方程式が存在しないなら、フェルマーの方程式は解を持たない。
4') ゆえに、フェルマーの最終定理は成り立つ。
フライの楕円方程式はモジュラーでないと証明することに、世界中の数学者は頭を抱えた。この線で動いている数学者の一人にカルフォニア大学バークレー校のケン・リベット教授がいた。1986年バリー・メーザーとリベットが討議して、「M構造のγゼロを加えるアイデアで、谷山・志村予想が成り立てばフルマ―の定理も成立する(すべての楕円方程式がモジュラーになれば、フェルマー方程式には解がない)ことにつながった。こうして数学者たちは、背理法を使ってフェルマーの最終定理に挑戦できるようになった。これまで30年以上も谷山・志村予想に挑戦して失敗してきた歴史を乗り越えたのがワイルズだったのである。楕円モジュラー複素関数の、クライン関数、ラムダ関数、世面体関数、イーター関数、アイゼンシュタイン関数の画像が面白いので参考のために示す。とにかく楕円関数論は面白く今なおホットな領域である。



5章をまとめると以下になる。谷山・志村予想は、1955年9月に日光の国際シンポジウムで谷山豊が提出した2つの「問題」(問題12と問題13)を原型とする。これらの問題が互いに関連しているらしいことは谷山も気付いていたが、実は同じ命題の言い換えであることが後に判明した。谷山自身は若くして自殺したため、1960年代に谷山の盟友である志村五郎によって、代数幾何学的な解釈によって正確に定式化された。その後、1967年のヴェイユによる研究によって広く知られるようになった。内容的に「ゼータの統一」というテーマを扱う豪快な予想であり、数論の中心に位置するものの一つと目されるまでにいたったが、攻略自体は絶望視されていた。1984年秋、この予想からフェルマーの最終定理が出るというアイディアがゲルハルト・フライにより提示され、セールによる定式化を経て(フライ・セールのイプシロン予想)、1986年夏にケン・リベットによって証明されたことにより俄然注目を集めたが、アンドリュー・ワイルズを除いては、まともに挑もうとする数学者は依然として現れなかった。アンドリュー・ワイルズ(プリンストン大学教授)により、この予想はまず半安定な場合について解決された(1993~1995年)。ワイルズが1993年に発表した証明には一箇所致命的なギャップが存在したため、その修正に当ってはリチャード・テイラーも貢献した。1994年9月、ワイルズはギャップを回避することに成功し、修正された証明は翌1995年に2編の論文として出版された 。このことにより、ワイルズは谷山・志村予想の系であるフェルマー予想をも解決した。アンドリュー・ワイルズ は、半安定楕円曲線の谷山・志村予想を証明し、それによってフェルマーの最終定理を証明した。20世紀の偉大な数理論理学者ヒルベルトや、ワイルズの恩師コーツ教授らはフェルマーの最終定理には取り組まなかった。誰も谷山・志村予想を証明できるとは思っていなかったからである。労多くして功なしとして敬遠したのである。この第6章に至って初めてワイルズの研究の詳細に入る。30代になってワイルズは冒険をする気になった。楕円方程式とモジュラー形式に関するあらゆる数学を1年半かけてマスターした。フェルマーの最終定理に関係ない研究からは一切手を引き、学会にもあまり顔を出さなくなった。そして自宅に引きこもり集中した。ワイルズはこの証明を完全な秘密のうちに一人で仕事を進める決心をした。しかもコンピューターを使わず、鉛筆と紙と自分の頭脳だけで証明に挑んだ。その証明の出発点は「帰納法」という方法で、たった一つの証明だけで無限問題に向かう方法である。帰納法は高校時代に習ったように、次の二つの手順からなる。①最初の場合に命題が真であることを証明する。n=1 ②命題がある場合に真ならば、すぐ次の場合にも真であることを証明する。n'=n+1 ワイルズは無限に存在する楕円方程式の一つ一つが、無限に存在するモジュラー形式の一つ一つに対応することを帰納法によって証明することであった。そしてそのために19世紀フランスの天才エヴァリスト・ガロアに注目した。エヴァリスト・ガロア(1811-1832年)は数学への情熱以上に共和派革命に命を捧げ21歳にして銃弾に倒れた。ガロアは代数方程式の解を求める事であったが、2次方程式の解、3次方程式の解、4次方程式の解は19世紀以前に得られていた。ガロアは5次方程式の解を求める難問に挑戦した。ガロアの論文2通はフランス学士院のオーギュスト・コーシ―に送られガロアの才能が認められる機会になるはずであったが、論文の手直し中に行方不明になり、再度ジョゼフ・フーリエに提出したが受理さえされなかった。そして1832年5月30日銃弾に倒れた。ガロアの計算の中心にあったのは、群論と呼ばれる概念である。群の重要な性質に「群に含まれる二つの要素を演算によって結び付けた結果は、やはりその群の要素となる」という者がある。例えば整数は加法については群をなすが、除法については群をなさない。しかし「有理数は除法について閉じている」ということができる。ガロアが5次方程式に関する結果はその少数の解を要素とする群を構成したからである。谷山・志村予想を証明するためワイルズは楕円方程式の一つ一つがモジュラー形式とペアになることを示すためには、すべてのE系列とM系列の一つの要素が一致することを確かめ、それから次の要素の確認を行う方法を取った。無限に存在するE系列とM系列の順序として帰納法によって次々と関連づけが保証されていった。ガロア群を利用するというワイルズの戦略は谷山・志村予想を証明するための第1歩であったが、発表はせずコツコツと作業を続けた。1988年3月東京都立大学の宮岡洋一が微分幾何学からアプローチし、フェルマーの最終定理を証明したという報が駆け巡った。1983年数論的代数幾何学者のプリンストン高等研究所のフィールズ賞受賞者ゲルト・ファルティングスはさまざまなベキ数nに対するx^n+y^n=1の図形を調べて、複数個の穴が開いていることから、フェルマー方程式は有限個の整数解しか持たないという。ファルティングスは宮岡の論理の破たんを見抜いた。こうしてフェルマーの最終定理の証明はまた闇の中に消えた。1991年ワイルズは孤独な研究のなかで、楕円方程式の岩澤理論の修正によって打開を試みたが失敗した。フェルマーの最終定理の証明の研究ももう5年になった。
1991年以来、ワイルズはボストンで開かれた楕円方程式の専門家会議に出かけ、コーツとの会話でコリヴァキアン=フラッハ法という楕円方程式の分析法に注目して、その拡張に没頭する日々を送った。ある特定の楕円方程式ではコリヴァキアン=フラッハ法は帰納法ができたが、どの方程式にも当てはまるわけではなかった。楕円方程式はいくつかの族に分類され、一つ一つの族にたいする適応を試みてゆき、楕円方程式の族がモジュラーであることが証明されていった。しかしコリヴァキアン=フラッハ法の厳密性を検証するため、1993年ワイルズはその幾何学的性質について専門家に意見を聞くことにした。その相談相手はプリンストン大学のニック・カッツ教授であった。検討すべきワイルズの内容が膨大であったため、ニック・カッツ教授は大学院生を対象とした講義形式を採用した。講義名は「楕円曲線の計算」とした。こうしてニック・カッツ教授はコリヴァキアン=フラッハ法の適用には誤りはないことを保証した。1993年5月バリー・メーザーの論文を読んでいて19世紀の構成法が楕円方程式の族に適用できそうだと分かった。これがフェルマーの最終定理を説くことの最終的決め手になったという。こうして7年の秘密研究の結果、谷山・志村予想の証明が完成した。1993年6月末ケンブリッジ大学ニュートン研究所において専門会議を開催し、そこで発表する手はずが整った。フェルマーの最終定理のことは伏せて「L関数と数論」というワークショップであった。この会議には主催者側にコーツ教授、招待者にはバリー・メーザー、ケン・リベット、コリヴァキアンらが続々集まってきた。彼の証明を支える理論を生み出した人々は全員そろっていた。ワイルズが何を話すか、噂は噂を読んで聴講者が集り会場はあふれて廊下で立ち聞きの状態であったという。ワイルズの講演は「モジュラー形式、楕円曲線、ガロア表現」という題目であった。公演は3回にわたって行われたが、第1回の講演後から研究者間のメールが飛び始め、興奮が沸き起こった。第3回の講演が終わった翌日ニューヨークタイムズ、ガーデアン、ル・モンドそしてテレビが一斉に「フェルマーの最終定理解決される」を報じた。メディアのお祭り騒ぎに一報で証明のチェックという重要な作業が進められた。ニュートン研究所でのワイルズの講演は証明の概略を示したにすぎず、専門家によって正式に認められたわけではない。ワイルズは論文を「インウエンチオネス・マスマチカエ」に提出し、編集人のバリー・メーザーはさっそく6人のレフリーの選出に取り掛かった。200頁の論文をを6つに分け、各レフリーが1章づつ担当した。小さな問題は著者とのメールでやりとりし解決していったが、コリヴァキアン=フラッハ法に関する問題指摘は簡単にはゆかなかった。ワイルズは9月になって問題が根本的な欠点であることに気が付いた。もっと証明を強化する必要があるというものであった。オイラー系コリヴァキアン=フラッハ法の共同研究者であったニック・カッツ教授も大いに悩み反省をした。メディアや数学研究者の間には「ワイルズの研究に欠陥か」という噂が出回っていた。この3章のレフリーを担当したのはリチャード・テイラーである。ワイルズは1993年12月4日メールでこの欠陥を認めた。「谷山・志村予想のセルマー群の計算に還元する基本的な部分は正しいのですが、モジュラー形式に付随する対称平方表現に関する半安定の場合でセルマー群の元の正確な上限を計算する最終段階が完全ではありません。2月に始まるプリンストン大学での講義でこの研究に関する完全な説明をするつもりです」と。ここからワイルズの証明は窮地に立たされた。1994年の冬はワイルズにとって絶望の淵にいた。論文を公開すると、アイデアを出した人に名誉を持ってゆかれるので、ワイルズは苦慮の末、この問題の専門家ケンブリッジ大学の講師リチャード・テイラーをプリンストンに招き共同研究することにした。ニュートン研究所での講演から14か月経過して、1994年9月19日、コリヴァキアン=フラッハ法に岩澤理論のアプローチが使えることに気が付いた。1994年10月25日二つの論文が発表された。
① 「モジュラー楕円関数とフェルマーの最終定理」 アンドリュ・ワイズ著 こちらの論文が主論文でフエルマーの最終定理の証明である
② 「ある種のヘッケ環の環論的性質」 リチャード・テイラー、アンドリュ・ワイズ著 この論文はオイラー系の構成に関するギャップ補完である。ヘッケ環が局所完全交差であるという仮定の下で完成された。オイラー系を削除したことで大分簡素になった。