 丂
丂
僶價儘僯傾擲搚斅亅亅亅亅惓曽宍偺懳妏慄偺挿偝偲僶價儘僯傾悢婰崋昞乮60恑朄乯丂
 丂
丂
棟宯弶妛惗岦偒偺悢妛偺柤挊偵丄媑揷梞堦挊丂乽楇偺敪尒乿乮娾攇怴彂丂1939擭乯偑偁傝傑偡丅僛儘偵傛偭偰悢偵亄丄亅偺曽岦偑梌偊傜傟丄10恑朄偱偺寁嶼偺妚柦偑婲偒傑偟偨丅媑揷梞堦巵偵傛傞偲乽傑偢幚梡揑偱宱嵪妶摦偵側偔偰偼側傜側偄寁嶼乮寁悢乯偲偄偆恖娫偺峴堊偼偳偆偟偰峴偭偰偄偨偺偩傠偆偐丅19悽婭巒傔偺僫億儗僆儞偺儘僔傾墦惇偱帩偪婣偭偨僜儘僶儞偼崱擔偺彫妛峑偺1擭惗偺嫵幒偵昁偢懚嵼偡傞寁悢婍乮嶼斦偺婎乯偵帡偰偄偨偲偄偆丅擔杮偱偼丄撉傒彂偒偦傠偽傫偼峕屗帪戙偺帥彫壆偱弾柉偺儕僥儔僔乕偲偟偰嫵偊傜傟偰偄偨丅惣儓乕儘僢僷偱偼300擭慜偵僜儘僶儞偼奺崙偺撈摿偺恑曕傪傕偭偰峀偔晛媦偟偰偄偨偲偄偆丅偲偙傠偑惣儓乕儘僢僷偱偼僜儘僶儞偑昅嶼偵偲偭偰戙傜傟偨丅偙偺昅嶼偵梡偄傜傟傞婰悢朄偼丄偦偺悢帤偼傾儔價傾悢帤偲屇偽傟偨丅傾儔價傾悢帤偺婲尮偼墦偔僀儞僪偵偁傝丄傾儔價傾恖偺庤偵傛偭偰儓乕儘僢僷偵傕偨傜偝傟偨丅変乆偺婰悢朄偼乽埵庢傝乿偵傛傞婰悢朄偱偁傞丅1偐傜9傑偱偺悢帤偺傎偐偵0傪壛偊偨10屄偺悢帤傪傕偭偰偡傟偽丄偳傟傎偳戝偒側帺慠悢乮惍悢乯傕彂偒昞偡偙偲偑偱偒傞丅嬻埵乮壗傕側偄偗偳埵偑忋偑偭偨報偵僛儘傪壛偊傞乯傪昞偡婰崋側偟偵偼埵庢傝偼偱偒側偄丅0偙偦幚偼僀儞僪婰悢朄偺妀怱偱偁傝丄戝偘偝偵尵偊偽恖椶暥壔偺執戝側堦曕偱偁偭偨偲偄偆偙偲偑偱偒傞丅屆戙僊儕僔儍丄儘乕儅丄拞悽僼儔儞僋墹崙側偳儐乕儘僢僷彅崙偱偼偮偄偵埵庢傝婰悢朄偼敪柧偝傟側偐偭偨丅僊儕僔儍偱偼傾儖僼傽儀僢僩婰悢朄偑峴傢傟丄偙傟偱偼戙悢妛偼偱偒側偐偭偨丅僀儞僪幃婰悢朄偼嵟傕10恑朄偵拤幚偱偁偭偨丅尰嵼擔杮偱変乆偑嫵傢偭偰偄傞柦悢朄偼10恑朄偱偁傞偑丄堦丆廫丄昐丄愮丄枩傑偱偼堦働僞忋偑傞偛偲偵悢柤偑曄傢傞偑丄偦傟埲忋偼孞傝曉偟師偼壄偲側傞丅偲偙傠偑僀儞僪柤悢朄偼堦寘忋偑傞偛偲偵拤幚偵柤慜偑曄傢傞偺偱偁傞丅僺僒偺僼傿儃僫僠乮慟壔幃偲偄偆僼傿儃僫僠偺悢楍偱桳柤乯偼1202擭乽僜儘僶儞偺彂乮寁嶼偺彂乯乿傪昞偟丄僀儞僪寁悢朄傗彜嬈寁嶼傪僀僞儕傾偵徯夘偟偨丅13悽婭傕枛偵側偭偰傛偆傗偔僀儞僪幃寁悢朄偑晛媦偟偨傛偆偱偁偭偨丅乿偲偄偆丅堦曽杮彂偺僥乕儅偱偁傞柺愊偼丄應掕偝傟偰弶傔偰柺愊偲側傞偺偱偁傞偑丄戝屆偺愄偵偼偦偺扨埵偼堦擔偱峩偣傞揷偺戝偒偝偱偁偭偨傝丄堦懇偺堫傪惗嶻偱偒傞揷偺戝偒偝偱偁傝丄堦愇晑帩偺傛偆偵壗恖偺恖娫偺惗妶偑梴偊傞偐偱偁偭偨傝丄揷偺斎偺挿偝偱偁偭偨傝偟傑偟偨丅柺愊亖廲亊墶偲偄偆寁嶼偑偱偒傞傛偆偵側偭偰丄偄傠偄傠側宍偺揷偺應検偵傛偭偰丄柺愊偺悢抣偑摨偠偱偁傟偽摍偟偄揷偲尒側偝傟傑偡乮旍梹搙丄棫抧忦審偼暿偲偟偰乯丅曽宍偲嶰妏宍偺搚抧乮墌宍偺搚抧偼寶抸忋堄枴偑偁傝傑偡偑乯偲偺岎姺傕壜擻偲側傝傑偡丅婭尦慜3000擭偛傠偐傜搒巗崙壠偑敪払偡傞偲丄崙壠巟攝婡峔偲偟偰姱椈乮悢妛偺怑恖乯偵傛傞搚抧偺寁應偍傛傃惗嶻検丄壽惻妟偺寁嶼乮崱偱偄偆偲擾悈徣丄捠嶻徣丄嵿柋徣娗妽乯偲婰榐丒摑寁偑峴傢傟巒傔偨丅忋偺恾偼儊僜億僞儈傾暥柧偺僶價儘僯傾抧曽傪巟攝偟偨僔儏儊乕儖掗崙帪戙偺擲搚斅偺恾偱偡丅曽宍偺搚抧偺寁應偲懳妏慄乮併2乯偺挿偝偺寁嶼寢壥傪60恑朄偱彂偄偨擲搚斅偱偡丅側偍僶價儘僯傾偺悢偺婰崋傕帵偟傑偡丅墌廃棪傕僺僞僑儔僗偺掕棟偲偄偆岞幃傕側偐偭偨帪戙偵丄偳偺傛偆偵寁嶼偟偨偺偐偼晄柧偱偡丅幚應偐傕抦傟傑偣傫丅巹払偼悢偺懱宯偼嵟弶偐傜偁傞傕偺偲偟偰丄帺慠悢乮惓偺惍悢乯丄惍悢丄桳棟悢乮惍悢偺斾乯丄柍棟悢乮彫悢揰埲壓偑塱墦偵懕偔暯曽崻側偳乯丄挻墇悢乮兾丄e側偳乯丄幚悢乮僨僨傿僉儞僩偺楢懕奣擮乯丄嫊悢丄暋慺悢嬻娫丄儀僋僩儖偲僥儞僜儖丄偲暘椶偟傑偡丅偟偐偟恖椶巎偲偟偰偼丄嵦廤惗妶偱帺慠悢傪敪柧偟丄崚暔惗嶻偲弌夛偭偰彫悢傗暘悢傪敪柧偟丄搒巗崙壠帪戙偺壿暭宱嵪偱晧嵚傪偁傜傢偡晧悢傪敪柧偟丄朿戝側戝偒偝偺悢傪寁嶼偡傞偨傔偵傾儔價傾悢帤傗僛儘傗10恑朄傪敪柧偟丄偦偟偰僛儘傪嫬偲偟偰僾儔僗偲儅僀僫僗偺曽岦傪帩偮悢偺嵗昗傪敪柧偟丄17悽婭偐傜惣墷嬤戙悢妛偺抋惗傪尒傑偟偨丅偦偟偰曽掱幃偺崻偲偟偰嫊悢偲暋慺悢傪摼傑偟偨偑曽岦傪帩偮悢偲偟偰擣抦偝傟傞傑偱悘暘帪娫偑偐偐傝傑偟偨丅偙偺傛偆側悢偺摦揑側揮岦偼傗偑偰丄儀僋僩儖傗峴楍傪惗傒弌偟傑偟偨丅柺愊傕摨條偱偡丅嬻娫傗恾宍傪懳徾偲偡傞悢妛偼婔壗妛偲尵偄傑偡偑丄傑偢偼僄僕僾僩偱峩抧傪應検偡傞偙偲偐傜巒傑傝傑偟偨丅偄傢偽乽寁検恾宍妛乿偱偡丅擾峩偺娭楢偱楯摥扨埵傗廂妌検扨埵偺柺愊偑掕媊偝傟傑偟偨丅壽惻偺懳徾偲偟偰姱椈偨偪乮彂婭乯偼柺愊偺堦斒壔傪峴偄丄廲亊墶偺挿偝傪婎慴偲偡傞悢抣偩偗偱張棟傪偟傑偟偨丅柺愊偑挿偝偲寢傃偮偄偰堦戙旘桇傪悑偘傑偟偨丅偙偺拪徾揑柺愊奣擮偼僶價儘僯傾搒巗崙壠偐傜尒傜傟傑偟偨偑丄嶰暯曽偺掕棟偑敪尒偝傟偨偺傕偙偺帪戙偱偡丅僊儕僔儍帪戙偺儐乕僋儕僢僪婔壗妛偼乽榑徹恾宍妛乿偲偄偆岞棟庡媊偲偟偰姰惉傪尒偰丄傾儖僉儊僨僗偵傛偭偰柺愊丄懱愊丄巇帠検丄嬋慄偺挿偝偺彅検傕嬫暘愊暘偲偟偰媮傔傞偙偲偑壜擻偲側傝傑偟偨丅偙傟偑旝暘丒愊暘妛偲偄偆夝愅妛偵側偭偨偺偼16悽婭埲崀偺帠偱偡偑丄柺愊偼岦偒傪帩偪曽岦傪帩偮傑偱偵側傝丄柺愊懍搙堦掕偺拞怱椡偑摥偔揤懱椡妛傗屆揟椡妛偵敪揥偝偣偨偺偑丄僈儕儗僀丄僯儏乕僩儞偺揤嵥偨偪偱偟偨丅偙偺傛偆偵偟偰尒傞偲丄擣幆偺恑壔偵増偭偰柺愊偼乽寁検恾宍妛乿偺悽奅偱惗傑傟丄乽幚懱恾宍妛乿偲偟偰敪揥偟偨丅堦斒惈丒拪徾惈偑崅偔側偭偰乽婔壗妛乿偲偟偰姰惉偟傑偟偨丅
侾乯丂搙検峵偺抋惗偙偺復偼丄擾峩偺巒傑傝偲丄巐戝屆戙暥柧乮儊僜億傾僞儈傾丄僄僕僾僩丄僀儞僟僗丄拞崙乯偲搒巗崙壠偺惉棫偵傛偭偰搙検峵偑惗傑傟傞帪戙傪奣娤偟傑偡丅塸岅偺count noun偲mass noun偼悢柤帉丄検柤帉偺偙偲偱偡丅mass偼庢堷偵偁偨偭偰偐偝傗栚曽傪昞偡傛偆偵側傝丄傗偑偰検堦斒傪昞偟傑偡丅暔棟偺悽奅偱偼乽幙検乿偱偡丅乽偐偝傗丄栚曽乿偐傜暘悢傗彫悢偑惗傑傟傑偟偨丅偟偐偟偦偺慜偐傜乽挿偝乿傪抦偭偰偄傑偟偨丅挿偝偺乽慺杙扨埵乿偵偼丄僄僕僾僩帪戙偐傜僉儏價僢僩乮榬広乯丄僶乕儉乮彾乯丄僨僕僢僩乮巜乯偑偁傝傑偟偨丅奺慺杙扨埵偵娭楢偑偱偒扨堦偺扨埵偱昞偟傑偟偨丅偙傟傪乽婎杮扨埵乿偲偄偄傑偡丅偙偙偐傜暘悢偲彫悢昞婰偑弌棃傑偟偨丅搒巗崙壠偺惉棫偵敽偄崙壠姱椈乮彂婭乯偑崚暔偺惗嶻検偲壽惻検傪寁嶼偟婰榐偡傞傛偆偵側傝傑偟偨丅偦偟偰挿偝丄悡丄栚曽偺慡崙摑堦乮拞崙偺婭尦慜3悽婭恅偺巒峜掗偵傛傞搙検峵偺惂掕偑嵟傕戝婯柾偱桳柤偱偡乯偑側偝傟傑偟偨丅搙偼暔嵎偟丄検偼瀍丄峵偼攭偺偙偲偱偡丅奺抧偺暥柧偺搙検峵偵偮偄偰埲壓偵婰偟傑偡丅
嘆丂僶價儘僯傾丗丂擾峩偑巒傑偭偨偺偼婭尦慜9500擭慜丄儊僜億僞儈傾偺惣偺儗償傽儞僩偵偍偄偰偱偡丅彫敒傗摛偺嵧攟愓偑尒傜傟傑偡丅巵懓嫟摨懱偺懞偑偱偒偨偺偼慜5000擭崰偲尵傢傟丄僔儏儊乕儖暥柧偑惗傑傟傑偟偨丅慜4000亅慜3侾00擭偺嬥愇婍暪梡帪戙偵燇燆偲孡偺摫擖偵傛傝旘桇揑偵怘椏偑憹嶻偝傟傞傛偆偵側傝傑偟偨丅恖岥偑憹偊丄幮夛暘嬈偑恑傒丄奒媺幮夛偑嶌傜傟傑偟偨丅僂儖僋婜乮慜3100乕慜2900擭乯偵巵懓嫟摨懱偑搒巗崙壠偲側傝丄撿儊僜億僞儈傾偵傾僢僇僪墹挬乮慜2344亅慜2154擭乯偑弌棃傑偟偨丅僂儖戞3墹挬乮慜2112亅2004擭乯偵偼僕僢僋儔僪偲偄偆嫄戝側恄揳偑寶愝偝傟傑偟偨丅僙儉懓偵傛傞僶價儘儞戞1墹挬乮慜1894亅慜1750擭乯帪戙偵僴儞儉儔價朄揟偑嶌傜傟傑偟偨丅偙偺屆僶價儘僯傾帪戙偼慜1595傑偱僇僢僔乕僩墹挬乮慜1550亅慜1157擭乯偑宲懕偟傑偟偨丅偙偺僶價儘僯傾帪戙偺搙検峵偺悢妛偼巟攝偺偨傔偺廳梫側惌嶔偲偟偰奐敪偝傟傑偟偨丅怘椘偺壽惻丄楯栶嶼掕崻嫆丄偦偟偰尃埿偺徾挜偲偟偰偺恄揳偺愝寁偺偨傔偵梡偄傜傟傑偟偨丅屆僶價儘僯傾帪戙偺挿偝偺婎杮扨埵偼僯儞僟儞丄僋僔儏丄僔儏僔乮1僯儞僟儞亖6m丂1僯儞僟儞亖12僋僔儏丂1僋僔儏亖0.5m榬広丄1僋僔儏=30僔儏僔巜広乯偱偟偨丅椃峴扨埵偵乮棦偵憡摉乯僗僞僨傿僆儞亖180m乮恖偑2暘娫偱曕偔嫍棧乯偑偁傝傑偡丅抧媴偺1搙亖600僗僞僨傿僆儞乮10800m乯偲偟偰偄傑偟偨丅懱愊偺扨埵偼僔儏働儖偱戝敒180棻偺懱愊偱偡丅栚曽偺扨埵傕摨偠僔儏働儖偱偡丅僔儏働儖偼暿偵僊儞偲屇偽傟丄8.36g偱偡丅600僊儖亖侾儅僫偱丄栺500g偱偟偨丅僶價儘僯傾偱偼偡偱偵嬧偑壿暭偲側偭偰偄偰丄壿暭偺扨埵傕僔儏働儖偱偟偨丅嬧偺壙奿偼嬥姺嶼偱崱偺20攞傎偳偺憡応偱偟偨丅
嘇丂僄僕僾僩丗丂僄僕僾僩偱戝敒丒彫敒丒摛側偳崚暔嵧攟偑巒傑偭偨偺偼慜5500亅4000擭偛傠偱丄愭巎帪戙偲屇偽傟傞丅慜4000擭乕慜3000擭傪愭墹挬帪戙偲偄傢傟丄忋偲壓僄僕僾僩偵墹挬偑偁偭偨偑丄慜3150擭偵僄僕僾僩偼摑堦偝傟戞1墹挬偑嶌傜傟丄戞2墹挬乮慜2890亅2686擭乯丄戞3墹挬乮慜2686亅2613擭乯丄戞4墹挬乮慜2613亅2498擭乯偲懕偒傑偟偨丅戞12墹挬偺僙儞僂僙儗僩3悽乮慜1878亅慜1841擭乯偼乽慡崙柉偵惓曽宍偺搚抧傪梌偊丄擭峷傪擺傔傞媊柋傪壽偟偨乿偲慜5悽婭偺僊儕僔儍偺楌巎壠僿儘僪僩僗偑彂偄偰偄傑偡丅偙偺墹偺恎挿偼4僉儏價僢3僶乕儉2僨傿僕僢僩偩偲偄偄傑偡丅1僉儏價僢僩榬広偼45.7cm偱偡偺偱丄俀m6cm偺挿恎偵側傝傑偡丅僄僕僾僩偺婰榐傾乕僼丒僷僺儖僗乮慜1800擭偺戞12墹挬帪戙乯偵偼暘悢偑搊応偟丄僺儔儈僢僪偺愝寁偑峴傢傟傑偟偨丅懱愊偺扨埵偼僿僇僩偱丄1僿僇僩亖3/40僉儏價僢僩棫曽乮7.17儕僢僩儖乯偱偟偨丅
嘊丂拞崙丗丂拞崙偱偼擾峩偑偼偠傑偭偨偺偼慜10000擭崰偲偝傟傑偡丅挿峕棳堟偱偼堫嶌偑庡偱偟偨丅慜5000擭偵偼丄攏壠昹暥壔偑尰傟丄椙弽暥壔乮慜3300亅慜2200擭乯偵堷偒宲偑傟傑偟偨丅墿壨棳堟偱偼嬄徺暥壔乮慜5000亅慜3000擭乯偑婲傝丄彫敒丄埦丄暷側偳偺擾峩丒庪椔丒嫏嬈惗妶偩偭偨偦偆偱偡丅壞墹挬乮慜2000亅慜1600擭乯丄壞傪柵傏偟偨焨墹挬偼慜1066擭偵惣廃偵柵傏偝傟丄惣廃偼慜770擭偵捛傢傟偰搶廃偲側傝傑偟偨丅師偄偱弔廐帪戙乮慜722亅慜481擭乯丄愴崙帪戙乮慜403亅慜221擭乯傪宱偰丄慜221擭恅偑慡拞崙傪摑堦偟丄壿暭丒搙検峵偺摑堦傪惉偟悑偘傑偟偨丅廃帪戙偺挿偝偺搙偼丄暘丄悺丄広丄忎丄堷偱偡丅栺2000擭慜偵10恑朄偑惍慠偲寛傔傜傟傑偟偨丅検偺扨埵偼庂丄崌丄彙丄搇丄澩偱偡丅乮侾彙亖1.8儕僢僩儖乯偙傟傕10恑朄偱偡丅廳偝偺峵偺扨埵偼丄珩丄椉丄嬕丄玎丄愇偱偡丅丂偙偙偱峵偼10恑朄偱偼側偔丄16椉偑1嬕丄30嬕偑1玎丄4玎偑愇偱偡丅乮1椉亖14.16僌儔儉丄1嬕亖226丏67僌儔儉乯丂
嘋丂僀儞僪丗丂僀儞僟僗愳偺棳堟偱擾嬈偑巒傑偭偨偺偼丄慜7000擭崰偱偡丅慜3500擭崰惣傾僕傾偐傜僪儔償傿僟恖偑僀儞僟僗愳棳堟偵恑弌偟儌僿儞僕儑僟儘偺搒巗崙壠傪抸偒傑偟偨丅儌僿儞僕儑僟儘堚愓偐傜愇奃娾惢偺暔嵎偟偑敪尒偝傟偰偄傑偡丅傾僼儕僇偺嶨崚偲摛偼儊僜億僞儈傾傪捠偠偰慜2350亅慜1800擭崰偵摫擖偝傟傑偟偨丅慜2000亅慜1500擭崰丄僐乕僇僒僗偺梀杚柉傾乕儕傾柉懓偑堏摦偟僀儞僪傪惇暈偟傑偟偨丅慜1000擭崰暥柧偺拞怱偼僈儞僕僗愳棳堟偵堏傝丄擾峩幮夛傪宍惉偟傑偟偨丅倠偺偙傠乽儕僌丒償僃乕僟乗乿偑惉棫偟傑偟偨丅慜5悽婭偛傠偺悢妛偲揤暥妛彂乽傾乕儖儎僷僥傿乕儎乿偵傛傞偲丄1僗儕乮恎挿広乯亖96傾儞僌儔乮巜暆1.9mm乯亖係僴僗僞乮榬広乯丄抧媴偺捈宎偼1050儓乕僕儍僫乮1.5624枩Km)偱偁傞偲婰偝傟偰偄傑偡丅儓乕僕儍僫=係僋儘乕僔儍偱攏偱峴偔堦擔偺峴掱偱偡丅僀儞僪偺僴儔僢僷堚愓偱敪尒偝傟偨惵摵惢偺暔嵎偟偼1栚惙傝偑9.3mm丄50攞偡傞偲僊儕僔儍偺侾僉儏價僢僩亖46.3mm偲側傞丅
柺愊偲偼塸岅偱area偲偄偄丄柺偺忋2師尦偺峀偑傝偱偡丅1師尦偑挿偝丄3師尦偑梕愊偲偺娭楢偱偡丅僄儕傾偼僒儞僗僋儕僢僩岅偺乽嬻偒抧乿傪岅尮偲偟偰偄傞偦偆偱偡丅塸岅偺僛儘偼摨偠偔僒儞僗僋儕僢僩岅偺乽嬻嫊乿僗乕僯傾傪岅尮偲偟偰偄傑偡丅僀儞僪偺僛儘偼8悽婭偺僑僂僞儅僔僢僟儖僞偵傛傞偭偲丄揰乽丒乿偱昞偝傟傑偟偨丅楌巎忋偼偠傔偰婰崋0偑尰傟傞偺偼僀儞僪杒晹偱弌搚偟偨柫斅偱876擭偲偝傟偰偄傑偡丅偟偐偟僇儞儃僕傾偱僔儍僇楋605擭丄僗儅僩儔偱庍夀楋608擭偺僛儘昞帵偑偁傝傑偡丅僀儞僪偺僛儘偼傾儔價傾偵擖偭偰傾儖僗傿僼儖偲屇偽傟丄儔僥儞岅偺僛僼傿儖儉偐傜乽僛儘乿偲側偭偨偲尵傢傟傑偡丅拞崙偱偼娍帤偺乽楇乿偼塉偺幋偺宍偵側偭偰偍傝丄10悽婭憊帪戙偵側偭偰弶傔偰暥專偵尰傟傑偟偨丅曽掱幃偺崻偼塸岅偱偼乽root]偱偡偑丄僒儞僗僋儕僢僩岅偺乽儉乕儔乿傪岅尮偲偟傑偡丅傾儔價傾偵偍偄偰偼偠傔偰巊梡偝傟偨偺偼丄9悽婭偺僀僗儔儉偺壢妛幰傾儖丒僼儚乕儕僘儈乕偲偝傟偰偄傑偡丅枹抦悢傪昞偡乽僕儍僪僁儖乿傪儖乕僩偲屇傃傑偟偨丅偙傟偑儔僥儞岅偐傜塸岅偲側傝乽儖乕僩乿偲側傝傑偟偨丅拞崙偱乽崻乿偑弌尰偡傞偺偼18悽婭偺偙偲偱偡丅柺愊偵偮偄偰偼僒儞僗僋儕僢僩岅偐傜偳偆曄慗偟偰僊儕僔儍偵揱傢偭偨偐偼晄柧偱偡丅僶價儘僯傾暥柧偺搒巗崙壠僇僢僔乕僩帪戙乮慜1746亅慜1173擭乯偺墌摏報復偵丄楻搇晅偺嗖乮彌乯偺恾偑崗傑傟偰偄傑偡丅戝敒180棻傪1僔儏働儖偲偟偰丄偙傟傪嶵偔敤偺柺愊偑1僔儏働儖偺峀偝偱偟偨丅侾僔儏働儖亖1僊儞亖0.6暯曽m偩偲尵傢傟傑偡丅1僊儞亖侾80僙,偮傑傝戝敒堦棻傪嶵偔峀偝偑乽僙乿偱6cm暯曽偱偡丅僴儞儉儔價墹挬偺屻婜乮慜16悽婭乯偺擲搚斅偵乽挿偝偲暆傪偐偗傞偲柺愊偵側傞乿偲彂偐傟偰偍傝丄挿曽宍偺媮愊岞幃偑抦傜傟偰偄傑偟偨丅柺愊偺扨埵偼乽僒儖乿偱丄侾僒儖亖1曈偺挿偝1僯儞僟偺惓曽宍偺柺愊偱偡丅1僯儞僟亖5.952m偱偡偺偱丄1僒儖亖36暯曽m偱偡丅僄僕僾僩偵傕柺愊偺扨埵乽僙乸偑偁傝傑偡偑6暯曽m偱偟偨丅僶價儘僯傾偺10攞偺峀偝偱偡丅僄僕僾僩偵偼儕儞僪偺僷僺儖僗偲偄偆寁嶼偺彂偑偁傝傑偡丅摑堦撿杒僄僕僾僩偺15墹挬墹儔乕偺帪戙偺尨彂偲尵傢傟傑偡偺偱丄慜1650擭慜偺彂偱偡丅偙偺彂偵偼侾働僢僩暯曽亖1僙僞僢僩亖1000僉儏價僢僩乮2646m~2)偲側偭偰偄傑偡丅10僉儏價僢僩暯曽亖儀働僀僗乮27.46m^2)偲偄偆扨埵傕偁傝傑偡丅擾峩偺奐巒偵敽偄丄楯摥傗廂妌偲娭楢偟偰丄柺愊偑堄幆偝傟傑偟偨丅偳偺抧堟偱傕柺愊扨埵偼擾峩偲晄壜暘偺娭學偵偁傝傑偡丅嵟弶偼楯摥傗廂妌偺扨埵偱偁偭偰丄柺愊偑挿偝偲偟偰應掕偝傟傞偺偼傕偭偲偺t偺帠偱偟偨丅
嘆丂廂妌偱應偭偨擔杮偺柺愊丗丂 擔杮偱偼丄701擭偺乽戝曮棩椷乿偺拞偵乽揷偼丄挿偝30曕丄峀12曕傪抜偲偣傛丄10抜傪挰偲偣傛乿偲彂偐傟偰傑偡丅1曕偼1.8m丄挰偺1曈偼108m偱偡丅抜偼54m亊21.6m偺挿抧宍偱丄柺愊傕挰傗抜偺扨埵偱應傜傟傑偟偨丅9悽婭敿偽偺乽椷廤夝乿偼乽乽揷偼挿偝30曕丄峀12曕傪抜偲偡傞丅抜愊偼360曕乿偲彂偐傟偰偄傑偡丅偙偺抜愊偺曕偼挿偝偱偼側偔柺愊偱偡丅侾曕偺柺愊偼1.8m亊1.8m偱忯2忯暘偮傑傝堦捸偺偙偲偱偡丅曕偲偄偆柺愊扨埵偼戝晇棩椷偵偼側偔丄拞崙偺乽嬨復嶼弍乿偺塭嬁偱偡丅乽嬨復嶼弍乿偵偼丄抜丄挰偲偄偆柺愊扨埵偼偁傝傑偣傫丅乽廲亊墶傪柺愊偺曕悢偲偡傞丅偙偺曕悢傪240偱妱傞偲悿偺悢傪摼丄100悿傪侾崰偲偡傞乿偲偁傝傑偡丅抜丄挰偼擔杮撈帺偺柺愊扨埵偱偡丅曕偲偄偆柺愊傪360偱妱傞偲抜悢傪摼傞丅偙偺1抜偺崻嫆偼廂妌検偲娭學偟傑偡丅乽1抜偼丄50懇偺堫傪摼傞丅侾懇偺堫傪鋗偲暷5彙傪摼傞乿偲乽椷廤夝乿偵彂偐傟偰偄傑偡丅1抜偱50懇偺堫傪摼傑偡偺偱丄250彙偺暷偑偲傟傑偡丅摉帪偺侾彙偼720ml乮4崌時偺梕愊乯偱偟偨偺偱丄1抜傛傝崱偺100彙偺暷偑摼傜傟傑偡姺嶼偲側傝傑偡丅1擔3崌偺斞傪怘傋傞偲偡傞偲侾擭娫偱100彙乮1愇乯偵憡摉偟傑偡丅偮傑傝恖堦恖傪梴偆暷偺惗嶻検傪摼傞揷偺峀偝偑1抜偩偭偨偺偱偡丅峕屗帪戙偺晲巑偺榎崅偺乽晑帩乿偼丄1擔屲崌偺暷傪婎杮偲偟傑偡偺偱丄堦恖晑帩偲偼1.825愇偲側傝傑偡丅689擭偺乽旘捁忩屼尨椷乿傑偱偼揷偼乽戙乿偱昞偟丄偦傟埲崀偵挰丆抜偺忦棦惂偵側偭偨丅1戙偼廲墶6曕乮48m暯曽乯偺惓曽宍傪5摍暘偟偨傕偺偱偡丅1戙偲偼1曕偺搚抧偱丄1懇偺堫偑庢傟傞揷偺峀偝偱偁傞丅1懇=10攃丂侾攆=10 埇丄1埇偲偼曅庤偱堦埇傝偟偨堫偺懇偱偡丅乽10埇傂偲攃偘乿偲偄偆尵梩傕偙偙偐傜偒偰偄傑偡丅忦棦惂偵側偭偰乽戙乿偺柺愊扨埵偼愓宍傕側偔柍偔側偭偨丅645擭戝壔偺夵怴偺徺偼崑懓巟攝偐傜揤峜偺捈愙巟攝傪嫮壔偟傑偟偨丅岞抧岞柉惂丒孲導惂丒屗愋丒寁挔丒斍揷廂庼偺朄丒慸梖挷偺惻惂傪嶌傞偙偲偲偟偰丄乽揷偼挿偝30曕丄峀偝12曕傪1抜偲偟偡傞丅10抜傪挰偲偡傞丅抜偛偲偵慸堫2懇2攃丄1挰偵偮偒慸堫22懇偲偡傞乿偲慸惻傪掕傔傑偟偨丅幚偼偙偺婰弎偼惓偟偔側偄丅1挰偵偮偒慸堫偼15懇偱側偗傟偽側傜側偄丅50擭屻偺乽椷廤夝乿偺棩椷傪愭庢傝偟偨婰弎偵側傝丄屻戙偺嶌暥偱偡丅晲椡僋乕僨僞乕傪傕偭偲傕傜偟偄惌帯夵妚偺傛偆偵尒偣傞偨傔偺媅憰偱偡丅戝壔偺夵怴偺徺偑偁偭偨偐偳偆偐傕媈傢偟偔側傝傑偡丅夵怴偺徺偑栚巜偡棩椷惂偼689擭偺乽忩屼尨椷乿傗701擭乽戝曮棩椷乿傪懸偨側偗傟偽側傝傑偣傫丅傑偨戝壔偺夵怴偲偄偆尵梩傕懚嵼偣偢丄峕屗帪戙枛婜偵埳払愮峀偑乽墹惌暅屆乿傪惓摉壔偡傞偨傔憿岅偟偨傕偺偱偡丅椷偺慜偺慶朄偱偼100戙偁偨傝3懇偺堫慸乮栺3亾偺壽惻棪乯偼丄壽惻偑搚抧偺廂妌偵傛偭偰應傜傟偰偄偨偙偲傪帵偟傑偡丅乽戝曮棩椷乿偼丄偙傟傪搚抧偵壽惻偡傞惂搙偵曄偊傑偟偨丅曄摦偡傞廂妌傛傝埨掕偟偨搚抧柺愊偵婎偯偔壽惻惂搙偵偟偨偺偱偡丅偮傑傝柺愊偺奣擮偼戙偵偟傠抜偵敀丄慸傪挜廂偡傞偨傔偵峫偊傜傟偨丅廂妌偺検偐傜峩嶌柺愊偵曄傢傝傑偟偨丅
嘇丂挬慛丒儌儞僑儖偺柺愊扨埵丗丂搶戝帥惓憅堾偵乽怴梾懞棊暥彂乿乮偩偄偨偄755擭偺嶌惢乯偲偄偆屆暥彂偑偁傝傑偡丅4偮偺懞偺摦懺挷嵏曬崘彂偱偡丅揤峜壠偑屆挬慛偺怴梾崙偵旘傃抧傪帩偭偰偄偨偺偐丄嫟摨奐敪抧偩偭偨偐偳偆偼偝偰偍偄偰丄柺愊偺應傝曽偵拲栚偟傑偟傚偆丅寢丄晧丄懇乮晧偼10懇丄寢偼100晧丄侾懇偼10攃丄攃偼10埇乯偲偄偆扨埵偑弌偰偒傑偡丅懇丄攃丄埇偼廂妌偺扨埵偩偭偨偺偑柺愊偺扨埵偵側偭偰偄傑偡丅拞崙偱偼斍屌偺乽娍彂乿偵傛傞偲丄偙偺崰偐側傝尩枾側挿偝傪婎弨偲偟偨柺愊扨埵偑妋棫偟偰偄傑偟偨丅偪傚偆偣傫偱偼拞崙偺惸崙偺惂搙傪摫擖偟挿偝傪婎慴偲偟偰偄傑偡丅廂妌傪婎慴偲偟偨寢丄晧丄懇丄攃丄埇惂搙偲丄柺愊偵傛傞曕丄悿丄晇丄壆丄堜偲偄偆惂搙偑崿梡偝傟偰偄偨偺偐丄尵偄姺偊偨偩偗偺帠偐偼晄柧偱偡丅偝傜偵屻悽挬慛偱偼楯摥偱應傞柺愊偑偁傝傑偟偨丅拞崙偺柧偺帪戙15悽婭偵乽挬慛晩乿偲偄偆彂暔偑偁傝傑偡丅媿堦摢偺椡偱巐擔娫偱峩偣傞柺愊傪寢偲偄偆婰嵹偑偁傝傑偡丅挬慛偱偼堦擔偺巇帠検傪擔峩丄栺2帪娫偺楯摥偱峩偣傞柺愊傪懅峩丄1帪娫摉偨傝偺巇帠検傪帪峩偲尵偄傑偟偨丅擾嶌嬈偺戝偒偝偱柺愊傪恾傞曽朄偱偡丅傑偨15悽婭拞崰偺乽悽廆幚榐乿偵傛傞偲丄揷偺廂妌検偐傜6摍媺偵暘偗丄揷広傪戞1揷広偐傜戞6揷広偵傑偱暿偗丄奺乆廃広傪寛傔傑偟偨丅1摍揷偺廂妌検傪100偲偡傞偲丄15亾偯偮尭偠偨摍媺偱偡丅梀杚偺柉偱偁偭偨儌儞僑儖偱偼丄楯摥傗廂妌傪婎慴偲偡傞柺愊傗嫍棧偺奣擮偑偁傝傑偣傫丅嫍棧偺奣擮偱偼堦擔偵堏摦偱偒傞嫍棧傪僱僂儕丄恞偵憡摉偡傞傾儖僞偲偄偆扨埵偑偁傝傑偟偨丅尦帪戙偐傜娍柉懓傪巟攝偡傞偙偲偵側偭偰丄娍柉懓偺惂搙傪偦偺傑傑摜廝偟偰偄傑偡丅
嘊丂僀儞僪丗丂庍夀偺揱婰偱偁傞乽僕儍乕僞僇乿偼慜5悽婭偛傠偺僈儞僕僗愳棳堟偺儅僈僟墹崙偺悈揷偺柺愊偺帠傪揱偊偰偄傑偡丅栶恖偑撽傪帩偭偰搚抧應検偵傗偭偰棃偨偲偄偆婰弎偑偁傝丄偁傞僶儔儌儞偑1000僇儕乕僒偺搚抧傪帩偪丄500僇儕乕僒丄50僇儕乕僒偺嬫暘傪峴偭偨偲偄偆丅1僇儕乕僒偱堦壠懓偑惗妶偱偒傞峀偝偩偲偡傞偲1傾乕儖慜屻偩偭偨偲巚傢傟傑偡丅12悽婭偛傠偺乽儕乕儔乕丒償傽乕僥傿乕乿偵傛傞偲,丄1償傽僢僔儍亖10僴僗僞偱4.65m丄20償傽僢僔儍巐曽偺搚抧傪侾償傽儖僞僫偲屇傃丄偦傟偼86.5傾乕儖偵憡摉偟傑偟偨丅6摢偺媿偱堦擔偱峩嶌偱偒傞峀偝偱偡丅偙偺彂偵偼嶰妏宍傗巐妏宍偺柺愊岞幃傗丄嶰暯曽偺掕棟傕弎傋傜傟偰偄傑偡丅搶撿僀儞僪偵孨椪偟偨僠儏乕儔墹挬乮9悽婭乕1267擭乯偼11悽婭偵嵟惙婜傪寎偊傑偟偨偑丄偦偺帪婜偺僸儞僘乕嫵帥堾偺暻柺偵丄柺愊扨埵偑婰偝傟偰偄傞偦偆偱偡丅婎杮扨埵偼償僃乗儕偱丄267傾乕儖丄偦偺1/2偑傾儔丄1/4偑僇乕儖丄1/20偑儅乕丄1/80偑僇乕擇丄1/320偑儉儞僨傿儕僴僀偱偡丅1儉儞僨傿儕僴僀亖8.3暯曽m傎偳偱偡丅
嘋丂楯摥偱應傞儓乕儘僢僷偺柺愊扨埵丗丂僀僊儕僗偵偼僄乕僇乕偲偄偆柺愊扨埵偑偁傝傑偡丅媿2摢嗖傪偮偗偰1擔偵峩偣傞峀偝偱偡丅僊儕僔儍岅偺擾抧傪昞偡傾僌儘僗偐傜偒偰偄傑偡丅傎傏摨偠柺愊傪昞偡扨埵偑奺崙偵偁傝傑偡丅僆乕僗僩儕傾偱偼儓乕働丄僴儞僈儕乕偱偼儓僢儂丄僪僀僣偱偼儐僢僿儖僩偱偡丅偙傟傜偺柤徧偼偄偢傟傕偔傃偒傪堄枴偡傞儔僥儞岅儐僌儉偐傜棃偰偄傑偡丅屆戙儘乕儅偵偼儐僌儉偐傜攈惗偟偨儐僎儖儉偲偄偆柺愊扨埵偑偁傝傑偟偨丅偡偱偵挿偝偲寢傃偮偄偨柺愊偱丄廲35.5m墶71m偺挿曽宍偺柺愊偱偡丅栺25傾乕儖偺峀偝偱偡丅僪僀僣偺僶僀僄儖儞抧曽偵偼敿擔偱峩偣傞儌儖僎儞偲偄偆柺愊扨埵偑偁傝傑偡丅儐僢僿儖僩偲摨偠峀偝偱偡丅僾儘僔傾抧曽偺儌儖僎儞傕傎傏1儐僢僿儖僩偱0.63僄乕僇乕偱偡丅侾擔偱峩偣傞柺愊偼僞乕僋丒償僃儖僋偲偄偄丄1.16僄乕僇乕丄1.878儐僢働儖僩偱偡丅僀僊儕僗偼婭尦慜500擭崰働儖僩恖偑嫃廧偟偰偄偰丄婭尦慜屻偼儀儖僈僀恖偑巟攝偟傑偟偨丅8摢偺媿偵傂偐偣傞嫮椡側嗖僇儖乕僇傪梡偄傑偟偨丅1悽婭偐傜3悽婭偵偐偗僀僊儕僗偼儘乕儅掗崙偵巟攝偝傟丄3悽婭枛偐傜僎儖儅儞柉懓偺傾儞僌儘偲僒僋僜儞恖偑怤擖偟偰巟攝偟傑偟偨丅僇儖乕僇偵傛傞峩嶌朄偑堷偒宲偑傟丄峩嶌抧偼挿曽宍偱偟偨丅13悽婭枛僄僪儚乕僪1悽偑偝偩傔偨1僄乕僇乕偼40.47傾乕儖偲偝傟丄姷椺朄偱偼1僄乕僇乕偼43500暯曽僼傿乕僩丄埥偼暆66僼傿乕僩丄挿偝660僼傿乕僩偺嵶挿偄抧偱偡丅廲墶斾偼1懳10偱丄僪僀僣偺儌儖僎儞偱傕摨偠偱偟偨丅
嘍丂惗妶扨埵偱應傞屆戙儘乕儅丗丂屆戙儘乕儅偵偼働儞僠儏儕傾偲偄偆柺愊扨埵偑偁傝傑偟偨丅侾働儞僠儏儕傾偼710m暯曽乮50僿僋僞乕儖乯偱丄71m暯曽偺僿儗僨傿僂儉100屄暘偐傜側傝傑偡丅僿儗僨傿僂儉偼悽廝抧偲偄偆堄枴偱偡丅侾僿儗僨傿僂儉偼儐僎儖儉偺2攞偱丄2摢偺媿偑堦擔偵峩偡峀偝偱傕偁傝傑偡丅儘乕儅偱偼働儞僠儏儕傾偼昐恖戉偲偄偆孯帠惂偲娭學偟丄孯恖1壠懓偵梌偊傜傟偨搚抧峀偝傪堄枴偟傑偡丅僊儕僔儍偱偼慜594擭僜儘儞偺幏惌姱偺帪巗柉傪4奒媺偵暘偗傑偟偨丅戞1巗柉偼儁儞僞僐僔僆儊僨傿僂儉僲僀偱500儊僨傿僂儉僲僀偺搚抧傪帩偮偲偄偆堄枴偱偡丅暷偺姺嶼偡傞偲143愇丄搚抧偺偺柺愊偱14挰偵摉偨傝傑偡丅戞2奒媺偼300亅500儊僨傿僂儉僲僀偱婻巑媺偱偡丅戞3奒媺偼200亅300儊僨傿僂儉僲僀僲僢僠傪帩偪擾柉偱偡丅戞4奒媺偼200儊僨傿僂儉僲僀埲壓偱楯摥幰媺偱偡丅僀僊儕僗偱偼帺桼柉1壠懓偑惗妶偱偒傞搚抧偺峀偝偼僴僀僪偲屇偽傟傑偟偨丅120僄乕僇乕丄48傊僋僞乕儖偱偡丅働儞僠儏儕傾偲傎傏摨偠柺愊偱偡丅偦偺懠僐儌儞偲尵傢傟傞嫟桳偺杚憪抧偺巊梡尃傕娷傒傑偟偨丅幮夛偺婎杮慻怐偱偁傞僴僀僪偑柺愊扨埵偵側偭偰備偔夁掱偵偼壽惻偺崌棟壔偺梫惪偑偁偭偨傛偆偱偡丅
嘐丂拞崙丗丂斍屌偺乽娍彂乿偵偼丄100曕傪侾悿丄100悿傪侾崰偲偡傞柺愊扨埵偑偁傝傑偟偨丅楯摥傗廂妌偲偼柍墢偺扨埵偱偡丅拞墰廤尃姱椈惂偺崌棟揑巚峫偼摥偄偰偄偨傛偆偱偡丅1崰偼1曈偑100曕偺惓曽宍偺柺愊偱偡丅挿偝偺1曕偑5広偱丄3広偑1m偱偡偺偱丄100曕偼167m丄1崰偼2.78僿僋僞乕儖偲側傝傑偡丅1崰偼侾晇丄3晇偑壆丄俁壆偑堜偱偡丅1堜偼侾棦巐曽偱偡丅1棦偼300曕丄500m偱偡丅1棦暯曽偼25僿僋僞乕儖偱偡丅慜21悽婭壞偺帪戙丄堦壠懓偵梌偊傜傟傞揷偼50悿偱丄慜16悽婭焨偺帪戙丄媼揷偼70悿丄慜11悽婭廃偺帪戙丄媼揷偼100悿偲側傝傑偟偨丅惻惂偼壞偺帪戙偺1/10傪廃偺帪戙偱傕堷偒宲偄偱偄傑偡丅搚抧偺僋儔僗偺忋拞壓偵傛偭偰媼揷偼100悿丄200悿丄300悿偲側傝傑偡丅
嘆丂乽嬨復嶼弍乿偲屆戙僶價儘僯傾丄屆戙僄僕僾僩偺媮愊朄丗丂偙偺復偼寁検恾宍妛偺栭柧偗傪弎傋傞偙偲偵側傞偺偱偁傞偑丄偦傟偼屆戙僊儕僔儍偺婔壗妛偺恑曕傪怳傝曉傞帠偱傕偁傞丅偦偺慜偵丄拞崙偺慜娍帪戙偺悢妛幰棲陘夆偑慜3悽婭偺恅帪戙傑偱偺嶼弍抦幆傪傑偲傔偨彂乽嬨復嶼弍乿偵偮偄偰弎傋偰偍偙偆丅乽嬨復嶼弍乿偼幚梡彂偱偄傢偽姱椈岦偗儅僯儏傾儖偺傛偆側墳梡椺偑拞怱偱丄惣墷偺壢妛偵條側榑徹恾宍妛偱偼偁傝傑偣傫丅偦偺拞偐傜丄戞1姫乽曽揷乿偱暘悢偺妱傝嶼乮儐乕僋儕僢僪偺屳彍朄乯丄戞9姫偺乽嬪屢乿偱僺僞僑儔僗偺掕棟乮嶰暯曽偺掕棟乯丄乽墌揷乿偱墌廃棪偲墌偺柺愊傪徯夘偟偰偄傑偡丅戞1姫乽曽揷乿偱丄挿曽宍偺揷偺柺愊傪埖偭偰偄傑偡丅墶15曕丄廲16曕偺挿曽宍偺揷傪侾悿乮240暯曽曕乯偲偟傑偟偨丅乽墶偺曚悢偲廲偺曕悢傪偐偗偰愊偺曕悢傪摼傞乿丂幚嵼偺戝偒偝偱偁傞柺愊偺應掕抣傪丄拪徾揑側悢偺惈幙乮偐偗嶼乯傪夘偟偰媮傔偰偄傞偺偱偡丅師偵廲墶偺應掕抣偑暘悢偺応崌丄偐偗嶼偺慜偵栺暘丒捠暘傪埖偄傑偡丅栺暘偼丄暘悢偺暘巕丒暘曣偺偆偪彫偝偄傎偆偱戝偒偄曽傪妱傝丄妱傝愗傟傞傑偱懕偗傞乽儐乕僋儕僢僪偺屳彍朄乿偲屇偽傟傑偡丅曽揷偺柺愊亖墶挿偝亊廲挿偝偲偄偆峫偊曽偑帵偝傟偰偄傑偡丅悢抣偺巐懃墘嶼偑柺愊偱傕捠梡偡傞偲偄偆傕偺偱偡丅捈愙應掕偱偒傞偺偼丄廲墶偺挿偝偱丄柺愊偼娫愙應掕偲尵偄傑偡丅柺愊偺戝彫偑搚抧偺峀偝偺戝彫丄摍壙丄岎姺偵棙梡偱偒傞偺偱偡丅偮偓偵戞9姫偺乽嬪屢乿偱僺僞僑儔僗偺掕棟乮嶰暯曽偺掕棟乯傪弎傋偰偄傑偡丅乽嬪偲屢偺奺乆傪帺忔偟偰壛偊偰暯曽偵奐偗偽丄尫偲側傞乿偲彂偐傟偰偄傑偡丅幬曈傪尫丄捈妏傪嫴傓曈傪嬪丄屢偲屇傇偺偱偡丅嶰暯曽偺掕棟偼忋偺幨恀乮嵍乯偵宖偘偨傛偆偵丄屆戙僶價儘僯傾偺擲搚斅乮慜2000擭崰乯偱惓曽宍偺懳妏慄偺挿偝偑60恑朄偱崗傑傟偰偄傑偡丅10恑朄偵捈偟偰撉傓偲1.4142129偲側傝丄併2偵傎傏堦抳偟偰偄傑偡丅併2偺奐偒曽偼丄慟師嬤帡寁嶼朄偺岞幃併(a^2+r)佮a+r/2s偱寁嶼偱偒傞偙偲傗丄乽僺僞僑儔僗偺僲乕儌儞乿乮恾宍偺暘夝堏摦乯傪抦偭偰偄偨傛偆偱偡丅徻偟偔偼戝栴恀堦挊乽僺僞僑儔僗偺掕棟乿乮搶奀戝妛弌斉晹丂2001乯傪嶲徠偟偰偔偩偝偄丅偮偓偵乽墌揷乿偱偼墌偺柺愊偺媮傔曽傪乽墌偺廃偺敿暘偲捈宎偺敿暘傪妡偗崌傢偣傞偲墌偺柺愊傪摼傞乿偲彂偐傟偰偄傑偡丅墌廃偺敿暘偼倢亖2兾倰/2偱丄柺愊S=乮2兾倰/2乯亊倰乮倰偼敿宎乯亖兾r^2偱惓偟偄岞幃偑摼傜傟傑偡丅乽嬨復嶼弍乿偱偼墌廃棪傪3偲峫偊偰偄偨偺偱岆嵎偼4.5亾彫偝偄丅愭偵彂偒傑偟偨偑屆戙僄僕僾僩偺彂傾乕儊僗丒僷僺儖僗乮儕儞僪丒僷僺儕僗乯偼慜17悽婭偺悢妛偺彂偱偡偑丄擾嶌暔偺攝暘傗攝媼偵寚偐偣側偄僄僕僾僩幃暘悢偺彂偲偟偰桳柤偱偡偑丄戙悢傗婔壗妛偵偮偄偰傕彂偐傟偰偄傑偡丅偲偔偵墌偺柺愊傪奜愙偡傞惓曽宍偺柺愊偺64/81偲偟傑偟偨丅惓曽宍傪嵶偐偔嬫暘偟偰備偔偲丄嬫暘偑彫偝偄傎偳椙偄嬤帡偑摼傜傟傑偡丅惓曽宍偺1曈傪9摍暘偟丄墌偺愯傔傞晹暘傪64彫嬫夋偲傒偨丅棟榑揑偵偼墌偺S=兾r^2丄惓曽宍偺柺愊S'=(2r)^2丂乮倰偼墌偺敿宎乯偡偺偱丄S/S'=兾r^2/4r^2=兾/4=3.141592丒丒/4=0.785398丒丒佮64/81=(8/9)^2(=0.79012丒丒)偲尒偨偺偱偟傚偆丅墌偺柺愊偲奜愙惓曽宍偺柺愊偺斾傪乽墌愊棪乿偲偄偄傑偡丅儕儞僪僷僺儖僗偵偼墌廃棪偺媈擮偼偁傝傑偣傫丅媡偵墌愊棪偐傜墌廃棪傪媮傔傞偲丄兾=4(S/S')偡側傢偪墐惾棪偺4攞偱偡偺偱丄墌廃棪偼3.16偲側傝傑偡丅師偄偱儕儞僪丒僷僺儖僗偼梕愊傪掙柺愊亊崅偝偲偟偰媮傔傑偟偨丅
嘇丂屆戙僊儕僔儍偺婔壗妛偲儐乕僋儕僢僪乽尨榑乿丗丂慜5悽婭偺屆戙僊儕僔儍偺儁儕僋儗僗幏惌姱帪戙偼妛弍怳嫽偑惙傫偲側傝丄僜僼傿僗僩偑妶桇偟傑偟偨丅僜僋儔僥僗丒僾儔僩儞傜偺揘妛幰偑攜弌偟傑偟偨丅儁儕僋儗僗偺巘偱偁偭偨傾僫僋僒僑儔僗偼慜480擭崰傾僥僱偱妶桇偟丄墌偺惓曽壔傪尋媶偟偨偲尵傢傟傑偡丅慜430擭崰傾儞僥傿億儞偼墌偵撪愙偡傞惓懡妏宍偐傜丄傾僩儌僗乮偙傟埲忋暘夝偱偒側偄偲偙傠傑偱摓払偡傞乯偺峫偊偐傜丄惓懡妏宍偺柺愊偑偮偄偵偼墌偺柺愊偵堦抳偡傞偲偟傑偟偨丅慜425擭崰妶桇偟偨僸僢僺傾僗偼擟堄偺妏傪3摍暘偡傞偨傔丄墌偵奜愙偡傞惓曽宍偺廲偺挿偝傪摍暘偟墌愊嬋慄傪摼傑偟偨丅儐乕僋儕僢僪偺掜巕偺僽儕儏僢僜儞偼墌偵撪愙偡傞惓懡妏宍偲奜愙偡傞惓懡妏宍傪峫偊偰丄曈偺悢傪尷傝側偔懡偔偟偰旝嵶暘偟傑偟偨丅傾儖僉儊僨僗偼偙偺曽朄傪棙梡偟偰丄惓96妏宍偵偮偄偰丄墌廃棪傪13.140845丒丒亙兾亙3.1428571丒丒傪摼傑偟偨丅儁乕僩儖丒儀僢僋儅儞挊丂揷旜梲堦栿丂乽兾偺楌巎乿乮偪偔傑妛寍暥屔2006擭乯偵傾儖僉儊僨僗偺曽朄側偳墌廃棪傪惛鉱偵媮傔傞偡傋偰偺曽朄偑昤偐傟偰偄傑偡丅偨偩墌偲摍偟偄柺愊傪帩偮惓曽宍傪傪嶌恾偡傞栤戣偼乽墌愊栤戣乿偲尵傢傟丄1882擭偵儕儞僨儅儞偑墌廃棪兾偑挻墇悢偱偁傞偙偲偐傜丄掕婯偲僐儞僷僗偐傜嶌恾偡傞偙偲偼晄壜擻偱偁傞寢榑偟傑偟偨丅慜5悽婭枛僸億僋儔僥僗偼捈妏嶰妏宍偺妏傪嫴傓2曈傪捈宎偲偡傞墌偲幬曈傪捈宎偲偡傞墌偑瀫偭偰嶌傞寧忬偺柺愊偺榓偑捈妏嶰妏宍偺柺愊偵摍偟偄偙偲傪敪尒偟傑偟偨丅偙傟傪僸億僋儔僥僗偺掕棟偲尵偄丄戝栴恀堦挊丂乽僺僞僑儔僗偺掕棟乿乮搶奀戝妛弌斉晹乯偵徻偟偔恾偑嵹偭偰偄傑偡丅僾僩儗儅僀僆僗墹挬偼傾儗僋僒儞僪儕傾偵恄揳儉僙僀僆儞偲晅懏恾彂娰傪寶偰傑偟偨丅偙偺恾彂娰偺尋媶堳偩偭偨儐乕僋儕僢僪偑慜3悽婭偵乽尨榑乿乮僗僩僀働傾乯傪挊偟傑偟偨丅尨榑偱媍榑偝傟偰偄傞偺偼恾宍偺惈幙偱偁偭偰丄寁検偲偼堦墳柍墢偱挿偝偼堦愗弌偰棃傑偣傫丅嶰暯曽偺掕棟傕弌偰棃傑偣傫丅弌偰偔傞偺偼嶰暯曽偺掕棟偲偼尵傢偢丄嶰惓曽宍偺掕棟偲偄偆暘妱堏摦偺婔壗妛偱偡丅嵵摗寷挊乽儐乕僋儕僢僪尨榑偲偼壗偐乿乮娾攇壢妛儔僀僽儔儕乕2008擭乯偵儐乕僋儕僢僪婔壗妛偺徯夘偑偁傞偺偱嶲徠偟偰偔偩偝偄丅柺愊偵偮偄偰儐乕僋儕僢僪偺庤朄傪棟夝偡傞偵偼戙悢偼梡偄側偄偱丄恾宍偺摍愊堏摦傪峫偊傟偽偄偄偺偱偡丅擇偮偺暯峴巐曈宍偺柺愊偼掙曈亊崅偝偺堦抳偲偄偆棟夝偱偼側偔丄掙曈傪嫟桳偟丄暯峴偺岞棟傛傝嶰妏宍偺崌摨傪尵偊偽嵪傒傑偡丅嶰妏宍偺摍愊堏摦偲偼掙曈偵懳偟偰捀揰偑暯峴堏摦
偡傟偽偦偺柺愊偼曄傢傝傑偣傫丅偙傟傪嶰妏宍偺摍愊堏摦偲尵偄丄乽嵸偪崌傢偣乿乮暘夝崌摨乯偱徹柧偟傑偡丅墌偼暘夝崌摨偱偒傑偣傫偺偱丄尨榑偵偼墌廃棪偼尰傟傑偣傫丅掙曈傪嫟桳偟丄嶰妏宍偺敿暘偺崅偝傪帩偮挿曽宍偺柺愊偲嶰妏宍偺柺愊偼摍偟偄偙偲傕摨條偱偡丅儐乕僋儕僢僪偺嶰惓曽宍偺掕棟偼戝栴恀堦挊乽僺僞僑儔僗偺掕棟乿偵彂偐傟偨捠傝偱偡偺偱徣棯偟傑偡丅尒帠偲偄偆偟偐偁傝傑偣傫丅婔壗妛揑夝朄偼曗彆慄傪彂偐傟傟偽昘夝偡傞偺偱偡偑丄偳偺傛偆側曗彆慄傪堷偔偐偑寛傔庤偱傂傜傔偒偑昁梫側偺偱偡偹丅嶰妏宍偺憡帡娭學偐傜斾椺偺掕棟偑尒偄偩偝傟丄擇偮偺憡帡側嶰妏宍偺柺愊斾偼憡帡斾偺帺忔偵側傞偙偲偼帺柧偱偡丅師偵挿曽宍偲摨偠柺愊偺惓曽宍偵捈偡偵偼乽曽檖乿偑栶偵棫偪傑偡丅偦偺慜偵墌偺捈宎傪幬曈偲偟捀揰偑墌廃忋偵偁傞嶰妏宍偼捀揰偑捈妏偱偁傞偙偲傪僊儕僔儍偺僞儗僗偑敪尒偟傑偟偨丅偦偺捀揰偐傜幬曈偵悅慄傪壓傠偟幬曈傪2偮偵暘偗傞丅挿偝傪a,b偲偟丄悅慄偺挿偝傪h偲偡傞偲丄擇偮偺嶰妏宍偺憡帡娭學傛傝丄h^2=a亊b偲偄偆娭學偑摼傜傟傞丅傛偭偰挿曽宍偺柺愊a亊b偵摍偟偄惓曽宍偺1曈偺挿偝h偑嶌恾偱偒偨丅
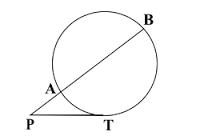
嘊丂僿儘儞偺岞幃丂丂寁検恾宍妛丗丂儐乕僋儕僢僪偺婔壗妛偼暘夝崌摨傪婎杮偲偟偰偄傞偑丄摨偠傾儗僋僒儞僪儕傾妛攈偺僿儘儞偺嶰妏宍偺柺愊岞幃偼戙悢妛偱偁傞丅嶰妏宍偺ABC偺捀揰A傛傝掙曈BC偵悅慄傪壓傠偟丄岎揰傪H偲偟丄AB=c,AC=b,BC=a=X+(a-x)偲偟偰丄s=a+b+c偲偡傞偲丄擇偮偺嶰妏宍仮ABH丄仮AHC偵僺僞僑儔僗偺掕棟傪傕偪偄偰h偲x偺楢棫曽掱幃傪夝偔偲丄嶰妏宍仮ABC偺柺愊偼S=(1/2)(ah)=併乮a(s-a)(s-b)(s-c)偑摼傜傟傞丅偙傟傪僿儘儞偺岞幃偲偄偆丅僿儘儞偺奐暯朄偼嵟弶偺嬤帡抣傪a偲偟丄曗惓傪h偲偡傞偲丄師偺嬤帡抣偼併A=a+h偲偟傑偡丅A=a^2+2ah+h^2偙偙偱h^2偼a偵斾傋偰彫偝偄偺偱h^2佮0偲偡傞偲丄師偺h偼乮A-a^2乯/2a偲側傝併A=(1/2)(a+A/a)丄偙傟傪壗夞偐孞傝曉偟偰奐暯偺嬤帡抣傪摼傑偡丅師偵2師曽掱幃偺崻傪曽檖偺掕棟偐傜嶌恾偡傞曽朄傪帵偟傑偡丅曽檖偺掕棟偲偼墌偺撪奜偺1揰偐傜2杮偺捈慄傪堷偄偰墌偲偺岎揰4揰傪摼傞帪丄尨揰偲墌偲偺岎揰傑偱偺嫍棧偺愊偑摍偟偄偙偲傪偄偆丅偦偟偰偦偺掕棟偺堦椺偲偟偰壓偺恾偵偍偄偰丄墌奜偺尨揰偐傜墌偵傑偠傢傞2杮偺慄偺偆偪堦偮偼墌偺拞怱傪捠傝丄堦偮偼墌偺愙慄偵側傞傕偺偱偡丅偦偺偲偒丄PT^2=PA亊PB偲側傝傑偡丅PT=a,PA=x-a,AB=a,PB=x偲偍偔丅偮傑傝捈宎a偺墌傪昤偄偰丄墌忋偺揰T偵偍偄偰愙慄傪堷偒PT-=a偲偡傞揰P傪掕傔傞丅偦偟偰P傛傝墌偺拞怱傪捠傞PAB傪堷偔偲丄PB=倶偑 x(x-a)=a^2偺夝偲側傞丅柺愊偼挿偝偺妡偗嶽偱偁傞偙偲傪帵偡丅
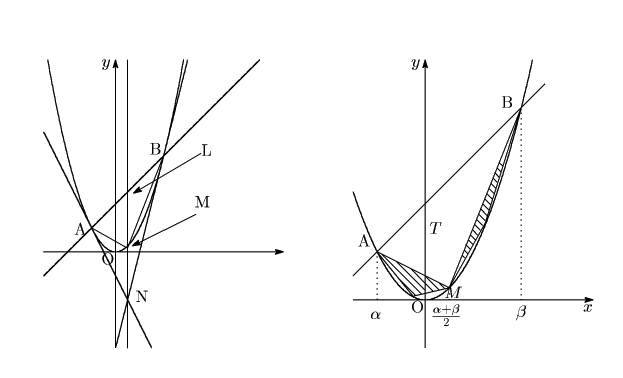
嬫暘媮愊朄乮棫懱偺懱愊傕傆偔傓乯偼僊儕僔儍帪戙僔儔僋僒僀偺悢妛幰傾儖僉儊僨僗偺岟愌偑戝偱偁傞丅嵵摗寷挊乽傾儖僉儊僨僗偺曽朄偺撲傪夝偔乿乮娾攇壢妛儔僀僽儔儕乕2014擭乯偵傾儖僉儊僨僗偺嬈愌偑傑偲傑偭偰偄傞丅傾儖僉儊僨僗偼丄尰戙偱尵偆愊暘朄偲摨偠庤朄偱柍尷彫傪棙梡偟偰偄偨丅攚棟朄傪梡偄傞斵偺徹柧偱偼丄夝偑懚嵼偡傞偁傞斖埻傪尷掕偡傞偙偲偱擟堄偺惛搙偱夝傪摼傞偙偲偑偱偒偨丅偙傟偼庢傝恠偔偟朄偺柤偱抦傜傟丄墌廃棪兾(僷僀)偺嬤帡抣傪媮傔傞嵺偵梡偄傜傟偨丅傾儖僉儊僨僗偼丄傂偲偮偺墌偵懳偟曈偑愙偟側偑傜偦傟傪偔傞傒擖傟傞戝偒側懡妏宍偲丄墌偺拞偱捀揰偑怗傟側偑傜偡偭傐傝廂傑傞彫偝側懡妏宍傪憐掕偟偨丅偙偺2偮偺懡妏宍偼曈偺悢傪憹傗偣偽憹傗偡掱丄墌偦偺傕偺偵嬤帡偟偰備偔丅傾儖僉儊僨僗偼96妏宍傪梡偄偰墌廃棪傪帋嶼偟丄傆偨偮偺懡妏宍偐傜偙傟偼栺3.1429偲栺3.1408偺娫偵偁傞偲偄偆寢壥傪摼偨丅傑偨斵偼丄墌偺柺愊偼敿宎偱偮偔傞惓曽宍偵墌廃棪傪忔偠偨抣偵摍偟偄偙偲傪徹柧偟偨丅亀媴偲墌拰偵偮偄偰亁偱偼丄擟堄偺2偮偺幚悢偵偮偄偰丄堦曽偺幚悢傪壗搙偐懌偟崌傢偣傞乮偁傞帺慠悢傪妡偗傞乯偲丄昁偢傕偆傂偲偮偺幚悢傪忋夞傞偙偲傪帵偟丄偙傟偼幚悢偵偍偗傞傾儖僉儊僨僗偺惈幙偲屇偽傟傞丅亀墌廃偺應掕亁偵偰傾儖僉儊僨僗偼3偺暯曽崻傪栺1.7320261偲1351偲栺1.7320512偺娫偲摫偄偨丅幚嵺偺3偺暯曽崻偼栺1.7320508偱偁傝丄偙傟偼旕忢偵惓妋側尒愊傕傝偩偭偨偑丄傾儖僉儊僨僗偼偙偺寢壥傪摫偔曽朄傪婰偟偰偄側偄丅僕儑儞丒僂僅儕僗偼丄傾儖僉儊僨僗偼寢榑偩偗傪帵偟丄屻悽偵懳偟偰曽朄傪偦偙偐傜堷偒弌偝偣傛偆偲偟偨偺偱偼偲峫嶡偟偰偄傞丅媴偺懱愊偼柍尷彫丒愊暘傪梡偄傞偙偲偱岞幃傪敪尒偟偨丅傑偨媴偺昞柺愊偼柍尷彫丒愊暘丒僇償傽儕僄儕偺尨棟傪梡偄傞偙偲偱岞幃傪摨偠崅偝偺墌拰偺懁柺偺昞柺愊偲摍偟偄偙偲傪帵偟偨丅傾儖僉儊僨僗偺棫徹偱偼丄偁傞捈慄偱嬫愗傜傟偨曻暔慄偺柺愊偼丄撪愙偡傞嶰妏宍偺柺愊偺4/3攞偵摍偟偔側傞丅亀曻暔慄偺媮愊朄亁偱傾儖僉儊僨僗偼丄曻暔慄偑捈慄偱愗傜傟偨晹暘偺柺愊偑丄曻暔慄偲捈慄偺岎揰偲捈慄偲暯峴側愙慄偑愙怗偡傞3揰傪捀揰偲偡傞嶰妏宍偺柺愊偺(4/3)攞偵側傞偙偲傪徹柧偟偨丅偙傟偼丄柍尷媺悢偲岞斾傪梡偄傞丅嵟弶偺嶰妏宍偺柺愊傪1偲偟丄偙偺嶰妏宍偺2曈傪妱慄偲偟丄曻暔慄偺寗娫偵摨條側庤抜偱2偮偺怴偟偄嶰妏宍傪憐掕偡傞偲丄偙偺柺愊偺榓偼1/4偲側傞丅偙傟傪柍悢偵孞傝曉偟偰曻暔慄偺愗曅傪庢傝恠偔偡偲丄柺愊偼仮ABM=(1/2)仮ABN偱偁傞偺偱丄師偺傛偆偵摫偐傟傞丅偙偺柍尷媺悢朄偼戝曄側楯椡偱偁傞丅偙偙偐傜傾儖僉儊僨僗偼崱堦曕偺偲偙傠偱夝愅妛偮傑傝旝愊暘朄傊恑傓偙偲偼偱偒側偐偭偨丅
 丂丂
丂丂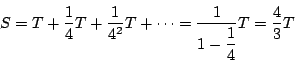
戞4復偼丄偙偙偐傜15暸傎偳崅峑偺悢妛嘨偺旝愊暘妛偲娭悢偺榖偵側傝丄嬫暘媮愊朄偲摫娭悢丄掕愊暘側偳傛偔抦傟偨偙偲偽偐傝偱丄摿偵夝愅妛傗娭悢榑傑偱撍偭崬傓撪梕偼側偄偺偱妱垽偟偨偄丅嵟屻偵儀僋僩儖夝愅偺撪梕偵側傞偺偱嫽枴怺偄偲偙傠傪徯夘偡傞丅悢捈慄偵傕僛儘傪嫬偵偟偰僾儔僗偲儅僀僫僗偺悢偑偁傞傛偆偵丄娭悢抣偑偑僛儘傪嫬偵儅僀僫僗抣乮晧悢乯傪庢傞傛偆偵側傞偲偦偺X幉偲偺娫偺柺愊偵傕惓偲晧偺曽岦偑惗偠傞丅偙傟傪柺愊儀僋僩儖偲偄偆丅偙偺曽岦乮儀僋僩儖乯偲戝偒偝乮僗僇儔乕乯偺婰榐偐傜丄崌惉乮嶰妏宍偺朄懃乯偲暘夝偺朄懃乮暯峴巐曈宍丄僗僥價儞偺朄懃乯偑惗偠傞丅XY嵗昗偱偺2夞偺楢懕偟偨曄埵乮A:a1仺B丗a2,:A丗b1仺B:b2)偵偼嶰妏OAB偵嶰暯曽偺掕棟傗戞2梋尫掕棟偐傜丄曄埵偺挿偝AB亖併乵乮b1-a1)^2+(b2-a2)^2乶丄儀僋僩儖偺撪愊OA丒OBcos兛=a1b1+a2b2偑媮傑傞丅媡偵撪愊偑僛儘側傜(兛=佢兾/2)2偮偺儀僋僩儖偼悅捈偱偡丅偦偙偐傜2偮偺儀僋僩儖偺嶌傞嶰妏宍OAB偺柺愊偼(1/2)OA丒OBsin兛=(1/2)(a1b2-a2b1) 丂3師尦嬻娫偱偼仮OAB=(1/2)併乵乮a2b3-a3b2)^2+(a3b1-a1b3)^2+(a1b2-a2b1)乶偲側傝傑偡丅恾偲儀僋僩儖婰崋傗峴楍幃側偟偵岅傞偙偲偼崲擄偱偡丅杮彂傪撉傫偱壓偝偄丅嵟屻偵僒僀僋儘僀僪嬋慄(墌傪捈慄忋偱揮偑偟偨嬋慄乯偲傾僗僥儘僀僪嬋慄偺柺愊偑柺敀偄偺偱庢傝忋偘傑偡丅寢壥偩偗傪尵偄傑偡偲丄僒僀僋儘僀僪嬋慄偵偮偄偰偼丄嘆墌偑1夞揮偟偨偲偒偺掕揰偺婳愓" 偺挿偝傪 l 偲偡傞偲丄l = 8rm乮= "捈宎" 偺 4攞乯丄嘇墌偑1夞揮偟偨偲偒偺掕揰偺婳愓" 偲 "x-幉" 偱埻傑傟偨晹暘偺柺愊傪 S 偲偡傞偲丄S = 3兾rm2乮= "墌偺柺愊" 偺 3攞乯丄嘊 3x幉傑傢傝偺夞揮懱偺懱愊傪 Vx 偲偡傞偲丄Vx = 5 兾2 rm3丂嘋x幉傑傢傝偺夞揮懱偺昞柺愊傪 Sx 偲偡傞偲丄Sx = (64/3兾)rm2偱偁傞丅
傾僗僥儘僀僪嬋慄偵偮偄偰偼丄嘆嬋慄偱埻傑傟偨柺愊偼 S =( 3/ 8) 兾丒a ^2 丄嘇嬋慄偺屖挿偼 l=6a偱偁傞丅
 丂丂丂丂丂
丂丂丂丂丂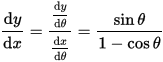 丂丂丂丂丂丂丂
丂丂丂丂丂丂丂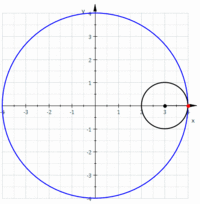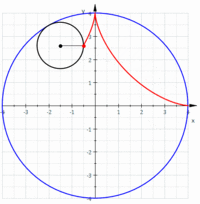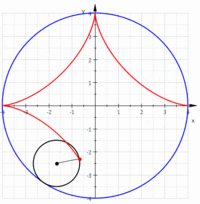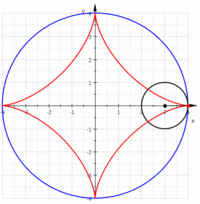 丂丂丂丂丂丂丂
丂丂丂丂丂丂丂