この本は肩の凝らない、不思議さと面白さを前面に出した数学への誘いの書です。だから数学の記号や数式の展開でつまずいてはいけません。そんなことはコケ脅かしで、（専門家になるためには必要ですが）数学が嫌になるきっかけに過ぎません。むしろ必要なのは数学が好きになるきっかけです。たとえば1と0.9は大きさが違う事は確かですが、1と0.9999999999・・・・（無限の9が続く）が同じであることも明白です。電卓の有効桁数7桁であれば、0.9999999と打つと１が表示されます。本書は数、形（空間）、無限の三点に絞って数学の楽しさ・摩訶不思議さを教えるくれるものです。私もこの10年間数学愛好者かどうかは知りませんが、金のかからぬ趣味として数学に関係する本を読んできました。物理問題は別にして、数学に関係する読書歴をあげてみます。その内容については項目をクリックすると要約を見ることができます。
1.　ゲーデル　著　「不完全性定理」　岩波文庫
2.　高木貞二　著　「近世数学史談」　岩波文庫
3.　高橋正仁　著　「人物で語る数学入門」　岩波新書
4.　ヒルベルト　著　「幾何学基礎論」　ちくま学芸文庫
5.　吉田武　著　「虚数の情緒―中学生からの全方位独学法」　東海大学出版社
6.　斎藤憲　著　「アルキメデス方法の謎を解く」　岩波科学ライブラリー
7.　斎藤憲　著　「ユークリッド原論とは何か」　岩波科学ライブラリー
8.　C・リード　著　「ヒルベルト―現代数学の巨峰」　岩波現代文庫
9.　坪田耕三　著　「数学的思考法」　岩波新書
10.　高橋正仁　著　「無限解析のはじまりー私のオイラー」　ちくま学芸文庫
11.　加藤文彦　著　「ガロアー天才数学者の生涯」　中公新書
12.　高橋正仁　著　「岡　潔　数学の詩人」　岩波新書
13.　高橋正仁　著　「高木貞二ー近代日本数学の父」　岩波新書
14.　二コラ・ブルバキ　著　「数学史」　ちくま学芸文庫
15.16.17　森　毅　著　「数学三部作ー数学の歴史（講談社学術文庫）、数学的思考法（講談社学術文庫）、異説数学者列伝（ちくま学芸文庫）」
18.　吉田武　著　「オイラーの贈り物」　東海大学出版社
19.　ベートル・ベックマン　著　「πの歴史」　ちくま学芸文庫
20.　吉田洋一　著　「零の発見」　岩波新書

我々は三次元の世界に住んでいると言われていますが、その三次元もあやふやで（X軸：右左、Y軸：前後、Z軸上下）、等速運動をしている二つの物体には運動は感じられませんし、地球に乗った自分が回転運動（自転、公転）をしていることも感じられません。ましてや四次元空間といっても想像もつきません。実物としての四次元空間を掴める人はいません。座標の三次元と時間を加えて四次元とよく言いますが、光より早く動くことのできな私達には過去の三次元空間を見ることはできません。すると多次元空間とは数学の想像上の空間に過ぎないのでしょうか。本書は想像力をキーワードにして、数学とはどんな科学なのかを考えさせる本です。本書を読み終わっても、どんな世界だったかとは実感できませんが、想像の翼を得て面白かったことは確かです。そこに魅せられた人々が数学者の列に加わることができるのでしょう。今の科学は数学の表現方法無しでは一歩も前に進めませんが、エジプトやメソポタミヤ文明では洪水の後の測量は生活共同体の必須の技術でした。今から三千年前には円周率や三角関数などは知られていました。アラビアス数字やゼロが発見されて人類の計算能力は飛躍的に向上しました。無限の数を計算することが出来ました。科学はまず観察することが人の最初の科学的行為だったに違いいありません。数学の出発点も他の科学と同じように、最初に出会う数学とは「物を数えること」です。物と、1，2，3を対応させることで物を数えたのです。多い、少ないは目で見て掴むことはできますが、どれだけだという量は数を対応させないと把握できません。文明前の人といえど、羊の数を1，2，3、それ以上は「たくさん」では生活できないし、まして交換は不可能です。数は人の想像力が作り出した抽象的な概念です。自然数1，2，3は個数を表現したり順序を表します。長さや重さなどの数えきれない量を表すために小数点や分数が登場します。そしてさらに高度化すると、一辺が1の正方形の対角線の長さはピタゴラスの定理から√2のような無理数が、また直系と遠州の長さの比較から超越数の円周率πが生まれました。無理数や超越数は無限にに続く循環しない小数です。分数は有理数といい等分することから生まれましたが、3/7というものがどんなことか現実社会とは縁の少ない数です。それは概念をイメージ化できるということは、抽象概念を具象化することです。イメージするために数学が用意したのは数学記号です。数学の想像力を自由に取り扱うための言語、それが数学記号です。ここから人間の頭の中の抽象操作が、計算（演算）という数学記号の世界に移し替えられるのです。と同時に個々の数はなくなり、一般化された係数や未知数という記号になり、演算規則に沿って並べられると方程式となります。これで一般性を獲得できるのです。図形の性質も三角形△ABCだけでは演算も何もできませんが、線分の比例関係、角度などの演算で代数に移し替えることができます。数学におけるリアリティも想像力によるイメージの展開を可能sにします。数学は想像力を数学記号と論理で操りイメージを膨らませる世界共通言語です。経験や読書をして私たちの世界は広がってゆきますが、数学という乗り物に乗って非日常的な世界を旅行することが可能になります。その「さわり」の不思議な世界を体験することが本書の目標となります。いまなぜか数学が人々の好奇心の対象になってきています。人々は「衣食足りて礼節を知る」ように、心の豊かさを求め、物の消費よりも、知的な関心を満たしてくれる抽象的な価値観に憧れてるようです。美的な価値観や心の価値観が優先するようになりました。文学や哲学、美術といった抽象的な分野の延長線上に数学を位置付けているようです。と言っても専門の数学者を除いては、一般市民が簡単に数学に親しむことができるわけではありません。ギリシャ時代アリストテレスのアカデミアは哲学・政治学を教えたところですが、門には「幾何学を知らぬ者はいるべからず」という額があったそうです。数学は量子物理学、宇宙物理学・工学の基礎をなしていますので、いい加減な定義や約束だけでは意味を成しません。それなりに基礎の理解が必要です。数学史という教養学の一分野があります。各分野ごとに独自の進化を遂げているために、数学史も、数論、代数学、幾何学、関数論、解析学、数理論理学などの分野の歴史が存在します。「数学とは何か」という問いは皆様方が受けた数学教育に沿って考えてゆくと分かりやすい。まず数の学問、次に形の学問です。幾何学とは形をどのような観点で見るかについての学問と言えます。空間の形は、小さな近似的平面ではユークリッド幾何学が紀元前3世紀のギリシャでまず最初に発展しました。数学の方法論はユークリッドの原論で論理で構成する論証つまり証明と定理が確立しました。地球規模になると球面幾何学や射影幾何学となり平行線が交わります。非ユークリッド幾何学の分野です。さらの宇宙の大きさになると、歪んだ空間となり現在目覚ましく理解が進んでいる分野です。相対性理論は最先端の数学が必要です。工学の分野では微積分学と微分方程式論が大活躍をします。数学を考えるための方法論も客観的な研究の対象となりました。背理法、帰納法・演繹法、三段論法、数値解析法、集合論と数理論理学が20世紀の現代数学を生み出しました。ヒルベルトの公理主義数学やブルバキの構造主義数学がそれです。本書では数学の全分野を扱うわけではなく、数、形と空間、無限と位相について見てゆきましょう。

数学の想像力が数学記号とっ論理の力を借りて、どのような世界を探求してきたのかを具体的に見てゆきましょう。まずはじめに、筆者の専門であったトポロジー（位相幾何学、広くは位相数学）を取り上げましょう。まず次元とは何だろうか。物理学との関係でいえば点Pの位置（座標）を表すP(x)は1次元、P(x,y)は2次元、p(x,y,z)は3次元、P(x,y,z,t)は4次元と言われます。0,1,2,3が点、線、平面、空間、時空間の次元と言われます。点の動きは平面では合成されてベクトルという大きさ（テンソル）と方向を持つ矢印となり、点)の運動を示します。ここまでは物理学の具象的なイメージを持つことができても、P(a,b,c,d,e,f,g,・・,n)N次元は理解できないでしょうから、定義を変えましょう。有る点（量）を決定する独立因子の数が次元だとすると、狭い空間を離れることができ急に一般化された気になります。形自身の自由度を次元といいます。点Pだけでなる世界は全く動くことはできませんので自由度はゼロです。つまりゼロ次元の世界です。次に曲線（直線も含まれる）を考えます。解析学では連続の関数として扱われますが、曲線も曲線状のある1点を基準にして、そこからの向きを持った距離で点Pの位置が粟わせます。従って曲線も一つの数値（パラメータ）で表すことができるので次元は1次です。直線、円は具体的な形としては2次元の平面の中でしか表すことはできません。らせん（弦巻き線）は1次元ですが3次元の空間でなければ具体的な像は描けません。円は曲線なので1次元の図形、しかもそれを実現できる空間は2次元の平面です。円を角度αというパラメーターであらわすと、x=cosα,y=sinαです。パラメーターα1個ですので1次元と言います。座標は(x,y)ですので平面でないと描けません。らせんの場合、x=cosα,y=sinα、Z=α（この場合αを時間tと考えれば時間と共に円周が上昇するらせんを描くことができます。パラメータはｔ1個で、座標は（x,y,z)3次元空間です。では2次元曲面はどうかというと、空間の中にある曲面上の点は3つの座標（x,y,z)が2つのパラメーターであらわされます。ですから2次元の図形です。鞍の曲面は双曲放物面と言います。このように空間の次元とは、その空間の中での点の位置を決定する座標の個数のことで、図形の次元とはその図形を表すために必要なパラメーターの個数の事です。

　　　　　　　　

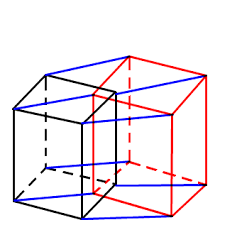
次に位相幾何学トポロジーの分野に移る。トポロジーとは「位相幾何学」や「位相数学」ともいう。 トポロジーは、数学の一分野であり、何らかの形（かたち。 あるいは「空間」）を連続変形（伸ばしたり曲げたりすることはするが切ったり貼ったりはしないこと）しても保たれる性質に焦点を当てたものである。トポロジーの分野で話題になる、クライン管、トーラス、メビウス帯、超立方体、クローバの結び目の画像の一例を上に示したので、まずその摩訶不思議さを堪能してほしい。各々の数式表現を示す。
クライン管：　x=(2+sinβ）cosα、y=(2+sinβ)sinα、z=cos(α/2)cosβ、w=sin(α/2)cosβ　（0≦α、β≦2π）
円周：　x=cosα、y=sinα　（0≦α≦2π）
球面：　x=cosαcosβ、　y=sinαcosβ、z=sinβ　（0≦α≦2π、-π/2≦β≦π/2)
トーラス（チューブ）：　x=(2+cosβ)cosα、y=(2+cosβ)sinα、z=sinβ　(0≦α、β≦2π）
メビウス帯：　x=(1+β/2cosα/2)cosα、y=(1+β/2cosα/2)sinα、z=β/2sinα/2　(0≦α≦2π、帯の幅-1≦β≦1)
四次元空間内の図形（変化する図形、運動する図形）を数学記号を使って考えてゆこう。想像力が捉えることができるという意味で具体的で、しかし手に触れることができるわけではない例を上の5つに関して図示した。左端に「クライン管（クラインの壺）」という図形があります。この曲面はトーラス（球体やチューブ）のように閉じていますが、内側と外側の区別がない曲面です。内側を歩いていたら外側に出ているという摩訶不思議な性汁を持っています。ポイントは穴です。（動物の消化器官は徹底して外腔です）　閉じているということは境界がないｋとで、閉じている曲面である球体やタイヤチューブには外と内の区別があります。風船になるのは内の空気が外へ出ないことです。ところが閉じているにもかかわらず、クライン管には内側と外側の区別はありません。クライン管は曲面なので図形としては2次元です（パラメータはα、βという2つの角度）。しかし3次元の空間でも表現することはできない不思議な曲面です。クライン管の数式表現では４つの座標（x,y,z,w)が二つのパラメータ(α、β）で表されています。円周を基本として数式を見てゆくと、球面は平面の円周を回転運動する点が上下にsin関数の運動が加わる図形であることが分かり、クライン管は円周上を回転運動している点が三角関数sin,cosの運動をすることが分かります。sinとcos関数は実はπ/2の位相差を与えると同じ関数ですので、クライン管は円柱の両端を4次元空間を使って反対側にひねってはり合わせたものです。閉じた曲線（輪ゴムを想像すると）を2次元空間で表すと、内側と外側の区別は厳格で曲線がその境界ですが、この輪ゴムを3次元空間におくと内側も外側の区別はなくなり自由に輪ゴムを通り抜けられます。これと同じように球面が3次元空間内にあると内側と外側の区別を持ちますが、これを４次元空間におけば球面は内と外の区別が消失します。クライン管がいわば「捻じれたトーラス」であることがわかります。そのため「メビウス帯」という図形を考えましょう。メビウスの帯とは細長い紙を一ひねりして張り合わせる形で、裏と表の区別の無い曲面です。メビウスの帯は3次元空間の中の曲面ですから、数式表現ではその1点は3つの座標(x,y,z)で表され、それぞれ座標が2つのパラメータ（α、β）で表します。βは帯の幅で、長さ1の線分が回転しながら原点の周りを1周する図形がメビウスの帯です。クライン管の表面にメビウスの帯を埋め込んだ図形ということができます。トーラスは捻じれていませんから埋め込むことはできませんが、メビウス帯は捻じれていますので埋め込むことができるのです。次元とは自由度の事で、その点の位置を示すために必要な数値です。この世界にはその点の様子を表すには4つ以上の変数が必要なものはいくらでもあります。世界は高次元空間から成り立っているようです。逆に、1，2，3個程度の変数で表される現象自体は、単純化された一側面しか見ていないようです。宇宙、生命体や経済は実に高次元の世界といえますが、それを表現する数学がないと言えます。

　　　　

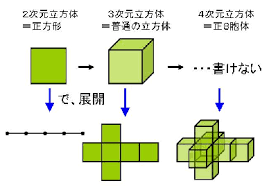
4次元空間は私たちの想像力の中にしか存在していません。ｎ次元空間も同じで抽象的なイメージの中から具体的な物を想像することで、数学記号と論理を駆使して現実世界との関係を見つけることが必要です。4次元の「超立方体」という図形を見てゆこう。立方体は正多面体の一つで、いわばサイコロの形です。見取り図、投影図、展開図の順にみますと、サイコロの外観が見取り図で、投影図は絵画でいう透視図法（射影幾何学）の事です。3次元の立方体はの表面は2次元の正方形を6枚組み合わせた図形です。これを展開図で表すこともできます。次元は自由度のことですから、0次元立方体は点です。１次元立方体は線です。２次元立方体は平面に書いた正方形（１次元の図形）です。３次元立方体はサイコロ（２次元の図形）です。では４次元の立方体（超立方体）とは何でしょうか。これは３次元空間（物理的空間）では表現できません。モデルとして上の右の投影図が参考になります。大小２つの正方形が入れ子になって８つの頂点が線分で結ばれた図形（台形）です。この台形は本当は正方形なのですが遠近法（透視図法）でみると台形のように歪んで見えます。投影図の中には、大小２つの立方体と小さい立方体を取り囲む６つの立法台形が見えています。これをほどいて見ると上の左図のように立方体からなる４次元超立方体の展開図が見えます。３次元空間の中での張り合わせは、立方体を歪ませなければできない。つまり第４の方向に曲げることで貼り合わせたのが４次元立方体の投影図です。するとn次元立方体（一辺の長さを１とする）の対角線の長さはピタゴラスの定理から√nですので、４次元立方体の対角線の長さは√４＝２となります。一辺が１のｎ次元立方体の体積がどんなに次元をあげても１であるのに、対角線はどんどん長くなります。集合論と超立方体との関係を見てゆきましょう。３つのもの方からなる集合X=｛a,b,c｝を考え、立方体の頂点（8つ）を、φ（ゼロ集合）、a,b,c,ab,bc,ac,abc(全体）の８つの要素とします。空集合φも全体Xも部分集合とすると、3次元立方体はこの部分集合同士の関係を図としてあらわしたものになります。これを４次元立方体に当てはめると、目の前にある3次元立方体が時間ごとに動いていると想像することができます。最後にトポロジーとしての結び目を考えましょう。例えば「クローバーの結び目」は切らない限り解けません。ところがクローバーの結び目が４次元空間に入っているとすると、この結び目は切ることなしに解けるのです。3次元空間の座標が時間ごとに平行移動すると分けなく結び目を通過できるのです。

数とは何か、とても難しい問題です。小学生に数を教えるには具体物を使って、（自然数、正の整数）を数え上げる、足す、引く、順序を教えます。単位となる物差しを使って長さを、ハカリを使って重さを、そして体積をと、実数の概念を拡大してゆきます。具体的ななものを通して表される数のイメージです。実数には小数がつきものです。整数とつぎの整数の間には実数が連続して詰まっています。中学生になるとピタゴラスの定理を教わりますが、正方形の一辺を１とすると対角線は√2=1.41421356・・・となり、際限なく小数が続き（無限小数）、これを無理数と言います。分数（n/m　整数）で表される数は有理数と言い、小数以下はある塊が循環します。これは整数が１から９の有限個であるからです。無理数が現れることになると中学生の数学きらいが始まります。無理数を含む実数を定義しようとすると急に抽象的になるからです。無理数の親戚に「超越数」があります。円周率π（円周/直径）=3.1415926535・・・・が最も有名ですが、これにπという名をつけたのが18世紀の数学者オイラーです。人がその数値を全部知ることはは永遠にできない。自然数は最初の約束事として公理を与え、そこから分数、整数、有理数、無理数、実数を順に構成してゆく。ここに公理と数学記号と論理に支えられた数論が生まれたのです。無限に続く数値を引きずっていては展開が困難です。そこで√2とかπという数学記号が生まれました。これを演算に使用することで実用性が生まれた。実数は量を表す数として考え出された。実在の量を使って数を表現した物、それが数直線です。ものさし（スケール）を想定すればいいのです。数をイメージとして理解しているのであって、数そのものを把握しているわけではありません。要するに数が存在するとは、抽象的な概念としてあるのです。√2が正方形の対角線の長さとして理解いれば、その数そのものは最後まで把握できなくてもいいのです。それと同じように虚数が量ではない何かを表す数（記号）として存在しているとしても何の不思議もありません。虚数が表すものそれは運動です。自然数が個数をあらわし、実数が長さなどの量を表すとすれば、虚数は回転を伴った移動を表すための数だと考えると、虚数が表すものが存在する。数直線上で我々はマイナスという数が向きを伴った数と解釈することを知っています。実数aに−1を掛けると、−aになります。これを反数関係といいます−1を掛けるということは数直線上では0を原点として180度変えるということです。掛けると１になるa×（1/a）関係を逆数関係と呼びます。次にx~2=-1（二乗したら−1となる数）のxをiで表します。i^2=-1なるiを虚数単位と言います。いま（x,y)の2次元座標を考え、y軸を虚数軸とし座標上での虚数の動きを見てゆきます。x軸の単位1に虚数iを掛けると1×i=iとなり、虚数軸上で虚数単位となり、x軸上の単位１は90度回転して虚数軸の上にあります。つぎに虚数の虚数を掛けるとi×i=i^2=-1となり、さらに90度回転してx軸上の−1に移動します。虚数が虚数軸上に表されるようになると、実数と虚数の和や積を考えることもできます。虚数は16世紀の数学者カルダノによって3次方程式の解法に使われました。虚数はイマジナリーナンバー、つまり想像上の数という意味です。時数と虚数の和を複素数z=a+bi(a,bは実数)と呼びます。複素数は数直線上には存在しません。実数軸（ｘ）と虚数軸（y)平面を複素数平面（ガウス平面）という。ここからオイラーの独壇場です。吉田武　著　「オイラーの贈り物」　（東海大学出版社）に詳しくオイラーの業績が示されているので、ここでは省略する。複素解析におけるオイラーの公式とは、に示される指数関数と三角関数を虚数が媒介して成り立つ等式をいう。　θ = π のとき、eiπ = -1 というオイラーの等式と呼ばれる式が得られる。この公式は複素解析をはじめとする純粋数学の様々な分野や、電気工学・物理学などであらわれる微分方程式の解析において重要な役割を演じる。物理学者のリチャード・ファインマンはこの公式を評して「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい，そして驚くべき「方法」」だと述べている。ここにeは自然対数の底でe=2.71828182845904、円周率πと同じく超越数と呼ばれる。超越数の命名の理由は、整数を係数とする代数方程式の解にはならない数を言う。円周率についてはベートル・ベックマン　著　「πの歴史」　（ちくま学芸文庫）に詳しいので省略する。オイラーは数値計算に関しては、πの仕事を全て終らせたといわれる。

√2や円周率だけでなく、数は無限問題と密接に絡んでいます。冒頭に取り上げた1=0.9999999999999・・・を再度取り上げましょう。例えば正方形を4等分に分割し、さらに4等分を繰り返した面積の和は1/3=0.333333・・・・・となります。これを級数であらわすと��(1/4^n)　n=1.,2,3,4,・・・ですので、等比級数の和を求める問題です。等比r=1/4ですのでその和はr/(1-r)=(1/4)/(1-1/4)=1/3です。いつまでも金魚の糞のように無限に続く小数点以下が付いて回ると計算になりません。そこで極限の概念が19世紀の数学で解決しました。使われる論理はε-δ論法といいます。たとえば１と0.999999との差は0.000001しかありません。この論法はずっと続きますので、１と0.9999999は異なる数字であるとは永久に言えないのです。差は無限小になってゆくので両者は同じ数と言っても差し障りはありまん。0.99999999・・・・→１またはlim(n→∞）��9/10^k=1と書きます。このように無限について極限という考え方は、微分積分学を始め数学に大きなインパクトを与えました。ガリレオは「新科学対話」の中で、自然数とその二乗の数はどちらが多いかという問いを出しています。1，2，3，4，5、・・・と1，4，9，16・・・・の数の集合の大きさを問うているのです。二乗の数は自然数の部分ですので、自然数の方が多いと答えそうなのですが、1と1、2と4、3と9，4と16はすべて1対1の対応が取れています。多い、少ない、等しいという属性は有限量のみであって、無限量にはない。つまり部分と全体は同じ大きさの集合なのだということになります。19世紀になってカント―ルが始めた集合論という現代数学がこれを解決しました。自然数は無限にありますが、カント―?は数え上げられた無限を全体としてとらえました。ある性質を持ったものを一つにまとめた集まりを「集合」と呼びます。集合の中に入るものを「元」とよび、｛x|ｘは性質pを持つ｝と書きます。これは記号です。無限個のものでも一つのまとめて集合が作れるのです。自然数NはN=｛n|nは自然数｝と表します。ガリレオは無限集合に対しては大きさを考えることはできないとしたのですが、カントルは「一対一対応の原理」で集合の大きさを考えました。個数を数える時の原則ですね。カントルは1対１の対応が付く以上、二つの集合は同じ大きさであるとした。しかし自然数の集合Nと実数の集合Rの大きさには違いがあるとカントルが発見した時に現代数学が誕生しました。小数全体の集合をXとします。通し番号をつけて数えられとして、それ以外にも別の小数がある事を対角線論法で背理法（私個人の考えは背理法は証明ではないと考えています。論理矛盾を導くだけで言葉の綾に過ぎないと思う）を使って導きました。数え上げあられる無限を可算無限と呼び、アレフゼロと呼びます。実数の無限は数え上げられなのでアレフゼロより大きい。これを連続体（デデキントの切断より）の無限といいます。「連続体の無限は?1である」という仮説を「連続体仮説」といいます。ヒルベルトは1900年の記念講演で今後解決すべき問題の筆頭に挙げています。
第1問題：ゲオルク・カントルによって提起された連続体仮説　「実数の部分集合には（高々）可付番集合と連続濃度集合の二種類しか存在しない。」
第2問題：算術の公理と無矛盾性　「算術の公理が矛盾を導かないことを証明せよ。」
第3問題：等底・等高な四面体の等積性　「等底・等高の四面体の等積性は、連続変形なしで証明できるか」
第4問題：直線が最短距離を与える幾何学の組織的研究　「公理がユークリッド幾何学に近い幾何学を求めよ。ただし行列の定理は保持し、合同定理は弱まり、平行線定理は省略されるものとする。」
第5問題：位相群がリー群となるための条件　「関数の微分可能性を仮定しないとき、リーによる連続変換群（リー群）の概念は成立するか。」
第6問題：物理学の諸公理の数学的扱い　「物理学は公理化できるか。」
第7問題：種々の数の無理性と超越性
第8問題：素数分布の問題、特にリーマン予想が正しいこと。すなわちゼーター関数という関数のゼロ点が負の整数を除いて、実部が1/2であること。
第9問題：一般相互法則
第10問題：ディオファントス方程式の可解性の決定問題

数学とは公式を憶え公式に当てはめて計算することだ受験数学では教えていたようです。数学が形式的な記号とその変形規則（演算）で成り立っていると考えるのも一理あります。しかしそれだけでは数学きらいを増やすだけです。日本で最低な教育は英語教育と数学教育です。電卓の登場（そして科学計算機能付き電卓）によって、その手書き計算能力さえおろそかになってきました。私達が計算技術を学ぶ大きな理由は、計算の構造を知り数の構造を知るためです。自然科学、特に数学の場合抽象性が増しますので、ますます何をやっているのかを自問することは重要です。現代数学では「公理」の位置づけは、すべての人が証明なしに納得できる枠組みから離れて、議論の出発点となる「約束事」になっています。しかし式の意味を考えることは数式の背後に広がるイメージを想像することです。数式を読むことは、それは数式の意味を理解することです。意味理解こそが数学的想像力を養うための要です。数学はその性格上すぐに抽象化されます。小学生はまず分数で躓きます。たとえば1/2と1/3を足すことは通分して分母を合わせてから、分子同士を足すことでおこない、必要なら最後に分子・分母を約分することです。メスシリンダーに水を足すことで考えると、メスシリンダーの目盛りを増やして6分の3の水に6分の2の水を足すと考えれば、答えは6分の5と納得ができます。割り算から速度、密度、濃度といったさらに抽象度の高い内容両概念に至ります。分数に分数を掛けるとか、分数を分数で割ることはもっとも小学生が戸惑う問題です。どこまで実体を想像するか、あるいは2，3の例で実体は判明したとして、後は機械的に計算するかそれは本人の納得のレベルの問題です。数学は形式を大事にする学問です。そして論理によって動かされています。数式の計算とは記号化された演繹論理の連鎖です。一カ所でも間違っていれば結果はすべて間違いです。ガリレオは「新科学対話」でこう言っています。「論理は推理の優れた手引きですが、発見への刺激智う点から見ると、幾何学に属する鋭い類別力には比べ物にならない」といいます。ニュートンが「プリンピキア」で徹頭徹尾幾何学で論を進めた理由がそれです。専門の数学者は論理の積み重ねから新しい発見に自動的につながるのではありません。自分が正しいと確信する結論に向けて、論理の鎖で正しいと証明されている知識と結びつけることを志します。そこにおける数学者の判断は直感的判断です。直感的判断を合理的判断に変えてゆくことです。想像することと形式的な記号と論理を操ることは数学の両輪です。幾何学は図形の性質を調べる学問ですが、想像力を広げて違う世界を展開したのはライプニッツでした。ニュートンと一緒に微積分の創始者として知られていますが、人の思想を記号で表し、記号を形成的に運用することで新たな世界を開拓しました。ライプニッツは位置解析は図形の性質を記号と論理の問題に還元しました。デカルト流解析幾何学は量の問題を図形の問題に変えました。位置解析を数学として取り扱ったのがオイラーです。オイラーは形のつながりという新しい幾何学を発見しました。点と点、線と線、面と面のつながり方を「ケーニヒベルグの橋の問題」の解法で示しました。形のつながりというテーマは19世紀末ポアンカレ―によってトポロジー（位相幾何学）という現代数学に発展しました。ポアンカレ―は形の本質とは何かという問題で、n次元まで拡大しホモロジー群、ホモトピー群という形式（群論）で表現しました。ここにユークリッド幾何学とは全く違った新しい幾何学が誕生しました。アメリカの数学者ミルナーは「エキゾチック球面」と呼ばれる7次元球面を作りました。この球面では微分の構造が異なり、関数の連続性が異なっています。数学の想像力は記号と形式、論理と一緒になってこんな不思議な形を想像したのです。普通のピンポン玉の表面は2次元の図形ですが、3次元空間の中でないと見えません。想像を絶する7次元の球面を数式という形式で取り扱うのです。この不思議な球面は4次元球面S4と3次元球面S3の直積S4×S3で表される図形を切って張り貼りかえますが、そのときに4次元という拡大複素数を使います。これらが数学的リアルティなのです。想像力の上に立つリアルなのです。バーチャルリアルティとはまた異なる世界です。

---