100531

物理学者ファイマン（「ご冗談でしょう　ファイマン先生！」の著書で知られている）がこういっている。
"We summarize with this,the most remarkable fomula in mathmatics: 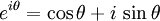this is our jewel"
数学、特に複素解析におけるオイラーの公式とは、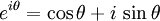に示される指数関数と三角関数を虚数が媒介して成り立つ等式をいう。　θ = π のとき、eiπ = -1 というオイラーの等式と呼ばれる式が得られる。この公式は複素解析をはじめとする純粋数学の様々な分野や、電気工学・物理学などであらわれる微分方程式の解析において重要な役割を演じる。物理学者のリチャード・ファインマンはこの公式を評して「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい，そして驚くべき「方法」」だと述べている。
私はこの本を題名だけで判断して、恐らく科学読み物か数学史くらいに考えて本屋に注文した。そして入手した本をぱらぱら見て驚いた。本格的な数学の専門本ではないかと疑った。ただし本格的な専門書は、この本のように内容的に間口はひろくないし、装丁も紙の質ももっと上質であるが。第１部でオイラーの公式を導くための数学の基礎全般を概説し、数論、級数、代数方程式、関数論、微分、積分を概説する。準備が整ったところで、第２部ではオイラーの公式の骨格をなすテイラー展開、指数関数と三角関数の特徴を概説する。そして第３部でオイラーの公式を導き、ベクトルと行列に応用して物理学への展開を述べる。付録としてアドバンスコースを設け、オイラーの公式の利用のすごさを実感してもらう過程となっている。今の数学教育ではお目にかかれない連分数や、√2、π、eが無理数である事の証明やフェルマーの最終定理など数論の基礎的話題は魅力に満ちている。４次までの代数方程式は何とか解けることの実習にかなりのページを割いている。行列形式による微分方程式の解法はベクトル形式を利用して物理学への重要な意味付けを扱っている。３行正法行列の行列式の計算とラプラ−ス変換による微分方程式の解法は有意義な勉強であった。本書はオイラーの式が持つ意味を理解するための総合的な数学入門であり、従来の分野別数学書ではない。私たちが大学の始めに習った名著高木貞治著「解析概論」のような格調の高さは無いが、紙と鉛筆、そして卓上電卓を座右において実践する数学として抜群の面白さがある。若い高校生が読めば、きっと数学が好きになるだろう。私のような高齢者が数学概論を勉強して何になるのかという疑問はあるが、いくつになっても面白いものはあるのだ。本の余白を数式の展開の鉛筆書きで満たす作業は、何物にも替え難い満足感を得た。まだまだ自分の脳は使えるのではないか？
「博士の愛した数式」(小川洋子著、新潮社、2003年)の中で出て来た博士の愛した数式とは、オイラーの公式と呼ばれるものです。ｅのπi乗に１を足すと0になるというものです。 このオイラーの公式を著者の小川さんは、以下のように表現しています。 「果ての果てまで循環する数と、決して正体を見せない虚ろな数が、簡潔な軌跡を描き、一点に着地する。どこにも円は登場しないのに、予期せぬ宙からπがeの元に舞い下り、恥ずかしがり屋のiと握手をする。彼らは身を寄せ合い、じっと息をひそめているのだが、一人の人間が1つだけ足し算をした途端、何の前触れもなく世界が転換する」と。
　吉田武氏の著書「虚数の情緒」に、オイラーの公式の三次元化が述べられている。一寸面白いオイラーの公式の視覚化なので紹介する。ｙｚ平面においては，パラメータを使った円の表現がなされており（半径１の円である）、ｘｙ平面にcosθのグラフ，ｚｘ平面にsinθのグラフが同時に描かれている。それをｘ軸方向に引き伸ばして，あたかもばねの様に立体化させたものがこの図である。

レオンハルト・オイラー（Leonhard Euler　1707 - 1783年）は18世紀最大の数学者・物理学者である。スイスのバーゼルに生まれ、ロシアのサンクトペテルブルクにて死去した。本書が紹介するオイラーの生涯を見て行こう。バーゼル大学でベルヌーイ（流体の運動方程式で有名）の講義に魅せられて、神学から数学へ転進した。19歳でパリ科学院のアカデミー賞に輝いたオイラーは勧められて、1727年ロシアのペテルスブルグに移った。女帝エカテリーナ1世の死去に伴う政情不安の中で、過度の勉強で右目を失明した。1741年ドイツのフリードリッヒ大王の招きでベルリン科学アカデミーに移り、素晴らしい研究成果を発表した。「無限解析入門」 と「微分学教程』」という数学書を出版した。1766年ロシアのエカテリーナ2世の要請で再びペテルスブルグに戻った。熱心な研究を続けたが、1773年白内障の手術を受けたものの、視力を失った。1783年天王星の軌道について議論中に逝ったといわれる。文学や社交には興味を示さず、数学と物理に専念した。オイラーは虚数iのみならず、πやeについて山ほどの公式を発見し、その普及には大きな功績があった。オイラーは数値計算に関しては、πの仕事を全て終らせたといわれる。ぺートル・ベックマン著「πの歴史」にオイラーのπの研究の業績が書かれているので紹介する。 オイラーの業績を見ると、まず解析学（無限小解析）においては膨大な業績があり、微分積分の創始以来もっともこの分野の技法的な完成に寄与した。級数や連分数、母関数の方法、補間法や近似計算、特殊関数や微分方程式、多重積分や偏微分法などなど、古典的な解析学のあらゆる部分に、基本的なものから応用にいたるまでの業績があった。私が大学に入ってからの5月病の原因であった高木貞治著「解析概論」の初めにはオイラーの業績が紹介されている。オイラーの名前は、指数関数と三角関数の間の関係を与えるオイラーの公式、オイラー＝マクローリンの和公式、オイラーの微分方程式、オイラーの定数などに残っている。フェルマー以降ラグランジュの出現までは進展がなかった整数論において、ほとんど一人で研究し続け、広大な結果を残した。数論的関数の一つであるオイラー関数に彼の名前が残っている。彼はゼータ関数と素数の関係を表すオイラー積の公式を発見、素数の逆数の和が発散するという新しい結果を得た。解析幾何学では一筆書きのできるグラフはオイラーグラフと呼ばれる。これはグラフ理論の起源となった。物理学では、ニュートン力学の幾何学的表現を解析学的に修正して、流体力学の基礎方程式（オイラーの連続方程式と運動方程式）を導いて体系化し、さらに剛体の力学を論じ、剛体に固定した運動座標系(オイラー角）を導入してオイラーの運動方程式を得た。

著者吉田武氏のプロフィールを紹介する。といっても吉田武氏に関する記事はなかなか見つからない。本書の末尾には「京都大学工学博士（数理工学）」」と書いてあるだけで、わかっていることは著者は京都大学教授であることだけである。経歴や業績の詮索はやめて、著書だけを紹介したい。稀に見る分厚い本を好んで書くユニークな先生で、本の読者は中学生を対象とすることが多いのが特徴である。しかしこんな難しい数学の本を並の中学生が理解できるとは思えないので、中学生でも理解できるように書いたという著者の試みは良しとしておこう。そして私の頭も中学生並みである事を白状しておこう。著者はかって「専門書の文庫化」ということを試みられたそうである。私は見たことが無いので、あまり普及しなかったようだが。
1999年　「ケプラーー天空の旋律」　（共立出版）
2000年　「マックスウエルー場と粒子の舞踏」　(共立出版）
2000年　「虚数の情緒ー中学生からの全方位独学法」　(東海大学出版会)
2002年　「はじめまして数学1、2、3」　（幻冬社）
2002年　「あの無限、この無限、どの無限？」　（日本経済新聞社）
2003年　「ノーベル物理学劇場ー仁科から小柴までー中学生の素粒子の世界」　(東海大出版会)
2005年　「私の速水御舟ー中学生からの日本画鑑賞」　(東海大出版会)
2006年　「はやぶさー不死身の探査機と宇宙研の物語」　（幻冬社)
2010年　「オイラーの贈り物ー人類の至宝eiπ=1を学ぶ」　(東海大出版会）
である。「虚数の情緒」については松岡正剛氏の「千夜千冊」に評論が出ているの、参考までに挙げる。

第1部の基礎編では、「パスカルの3角形」で2項定理と数列の面白さを、「方程式と関数」では2次方程式の解と虚数の登場と関数の性質を知るためのグラフの活用を、微分積分の定義と基礎公式を概説する。2，3の初歩的事項をあくまで丁寧に分るように具体的に説明する。これでは本のページ数が多くなるのはやむをえない。専門書のような、理解できない人には大きな壁を感じるような冷たさは無い。素数を求める「エラトステネスの篩」という方法を知った。連続という概念、循環小数を分数で表す方法は面白かった。これはもうビンゴゲームを超えるパズルといってもよい面白さがある。(a＋b)のn乗を展開する2項定理の係数が、相異なるｎ個のものからｒ個をとる順列組み合わせから求められる。上の二つの項の和であるパスカルの3角形の数列と前の2つの項の和で決まるフィボナッチの数列が、同じ数表の斜め読みでつながっていたのは、確かに当然である。数列が収束する条件と、等比級数、等差級数の和の公式はまさに天才技(奇想天外）である。2次方程式の解法で初めて虚数が登場する。関数とグラフ、微分積分は普通の高校の教科書と同じなので割愛する。又計算機で数値的に方程式の解をもとめるニュートンラプソン方は随分お世話になったので、その重要性はいうまでも無い。そしてこれが√の開法にもなっていたのだ。

第2部はオイラーの公式の三大構成要素である、テイラー級数展開と指数関数（対数関数）、3角関数の基礎を述べる。級数の和を求めることの逆で、ひとつの式を級数に展開できないだろうかn次高次代数方程式の微分を行なうと、ひとつづつ次数が減じていくことを利用してテイラー展開が可能となった。2項定理も改めてテイラー展開に含められた。指数関数は実に簡素化された性質を持つ。その最大の性質は微分をしても関数の形を変えないことである。そしてe0=1と定義するので（eはネイピア数という無理数）、そのテイラー展開はより簡素化されたxのベキ級数で表される。対数という関数は指数関数の逆関係にあり、微分すると1/xとなるという便利な形式をもつ。3角関数は円と切り離せないほどの関係があり、円の関数といってもよい。小川洋子さんが不思議がる必要もなく、πは角度θとみればオイラーの公式のひとつの特殊形であった。πも無理数である。本書によるピタゴラスの内接n正多角形によるπの漸次計算法は、連√形式ではあるが、ぺートル・ベックマン著「πの歴史」の説明よりずっと整理されていて分りやすい。周期関数である3角関数の諸定理は高校の教科書と同じであるので省略する。(cosx)2＋(sinx)2=1の解として、A=cosx＋isinx 　B=cosx−isinxとおけば、A,Bは指数関数と同じ性質をもつので、ド・モアブルの定理（cosx±isinx)n=cosnx±isinnxが得られて、3角関数、虚数、指数関数の間に密接な関係が見られ、オイラーの公式の準備が整った。3角関数もテイラー展開が出来ることはいうまでも無い。

A=cosx＋isinxを級数展開すると、指数をテイラー展開した形とおなじであり、ｘをiθに置き換えると、eiθ=cosiθ＋isiniθというオイラーの公式がえられる。ここでそれぞれ独立して定義された関数、単調関数である指数関数と周期関数である3角関数が虚数を取り込むことによって結びついている。そしてこの公式は調和振動子という物理学に直結するのである。θ＝π（180度）とおけば、eiπ=-1となり円周率とも手を結ぶのである。sinθ=1/2i(eiθ−e-iθ）,cosθ=1/2i(eiθ＋e-iθ）,tanθ=(eiθ−e-iθ）/i(eiθ＋e-iθ）と書き換えれば、3角関数の理論は複素平面(ガウス平面）上の指数関数に移され、指数関数の簡素な法則(微積分によって関数形を変えない）を利用して見通しのいい関係が出来る。オイラーの公式は複素数の幾何学（解析幾何学）そして極座標からベクトルへと応用される。オイラーは剛体の力学に回転の極座標を導入したことで有名である。ベクトルの代数表現として行列があるが、本書の行列についても大学1年で学習する行列と行列式の範囲を出るものではないので割愛する。単位行列と虚数行列(直交行列）を定義してオイラーの公式の行列表現ができる。そして微分方程式の行列解法になくてはならないケイリー・ハミルトンの固有方程式が2行2列の行列に関して導かれた。

第1部から第3部の解説において、煩雑を恐れて話題としなかった事項について、基礎をひととおり理解した段階でさらに高度な内容へ進むのがこのアドバンス・コースである。内容は多岐にわたり、22の事項が解説されている。整数論では最大公約数を求めるユークリッドの互除法という割り算の漸次アルゴリズムをBASICという言語でプログラムすることが述べられている。本文ではN=1または2の場合のみ詳しく解説して、Nの一般式を誘導しているが本当はその証明がなかった。これを証明するのが数学的帰納法である。これも高校で習ったところだ。素数が無限大に存在することを、数学的帰謬法で証明している。順列組み合わせの一般項の公式も高校で学習したことである。無理数、ネイピア数e、円周率π、黄金数を連分数で計算することを通じて、パスカルの3角形からフィボナッチ数列へ、フィボナッチ数列から黄金数へ、黄金数から円周率、ネイピア数へ、そしてオイラーの公式を通じて虚数へとひとつの橋が架けられた。数学的に重要な定数はお互いに暗渠で通じ合っていたとしか言いようの無い見事さであった。（これら定数はどうしても有理数にできない超越数という）　話題として3次以上のピタゴラスの定理をみたす自然数は存在しないというフェルマーの最終定理や、5次以上の代数方程式の一般的代数解法は無いことにこだわり続けた人々(ガウスはn次代数方程式は複素数の範囲にn個の根を持つことを証明したが、解法は知らないという）から、ガロア群論がうまれた契機となった。この第4部で4次代数方程式の一般的解法の解説に力を入れているようだ。三次のタルタニアーカルダノ解法、4次のフェラーリの解法とその演習である。行列による微分方程式の解法に随分ページを割いている。1階線形微分方程式の一般的解の公式を導いて、2階線形微分方程式を解くという手法である。例題として、物理学的に重要な問題、自由落下の方程式、強制調和振動子、減衰調和振動子の解法を説いている。そしてスカラー3重積から重要な性質を導き、三次の正方行列と行列式を解説している。これも大学1年で学んだ事項である。微分方程式の演算子法解法で、微分積分を考察する変数を複素数に拡張することによって、単なる代数計算に置き換えることができる。F(s)＝∫e-st・f(t)dt　これをラプラース変換という。定数、一次変数ｔ、指数関数、１階導関数、２階導関数のラプラ−ス変換などが出来るが、何でも出来るわけでなく、初期値問題では意外に応用が広い。